题目内容
 四棱锥P-ABCD中,底面ABCD是边长为8的菱形,∠BAD=
四棱锥P-ABCD中,底面ABCD是边长为8的菱形,∠BAD=| π | 3 |
(1)求四棱锥P-ABCD的体积;
(2)求证:AD⊥PB;
(3)若点E为BC的中点,能否在棱PC上找到一点F,使平面 DEF⊥平面ABCD,并证明你的结论?
分析:(1)四棱锥P-ABCD的体积=
×菱形ABCD的面积×棱锥的高,由平面PAD⊥平面ABCD,过P作PM⊥AD于M可得高PM,菱形ABCD的面积也可求;
(2)要证AD⊥PB,只需证AD⊥平面PMB,由AD⊥PM,AD⊥BM可证得;
(3)当点F为棱PC的中点时,面DEF⊥面ABCD;因为
【法一】,由AD⊥EF,AD⊥DE证得AD⊥面DEF,从而得面DEF⊥面ABCD;
【法二】,由FO∥PM,PM⊥面ABCD,证得FO⊥面ABCD,从而得面DEF⊥面ABCD.
| 1 |
| 3 |
(2)要证AD⊥PB,只需证AD⊥平面PMB,由AD⊥PM,AD⊥BM可证得;
(3)当点F为棱PC的中点时,面DEF⊥面ABCD;因为
【法一】,由AD⊥EF,AD⊥DE证得AD⊥面DEF,从而得面DEF⊥面ABCD;
【法二】,由FO∥PM,PM⊥面ABCD,证得FO⊥面ABCD,从而得面DEF⊥面ABCD.
解答: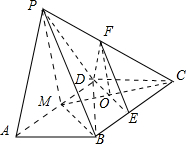 解:(1)如图
解:(1)如图
过P作PM⊥AD于M,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PM?平面PAD,
∴PM⊥面ABCD;
又PA=PD=5,AD=8
∴M为AD的中点,且PM=
=3,
∵菱形ABCD中,∠BAD=
,AD=8,
∴VP-ABCD=
×8×8×sin
×3=
×64×
×3=32
,
∴四棱锥P-ABCD的体积为32
;
(2)证明:连接BM,BD;
∵BD=BA=8,AM=DM,∠BAD=
,∴AD⊥BM,
又AD⊥PM,且BM∩PM=M,
∴AD⊥平面PMB,
∵PB?平面PMB,
∴AD⊥PB;
(3)能找到,并且点F为棱PC的中点,
证法一:∵F为PC的中点,点E为BC的中点,∴EF∥PB;
又由(2)可知AD⊥PB,∴AD⊥EF,
由AD⊥BM,BM∥DE,∴AD⊥DE;
又AD⊥EF,且DE∩EF=E,∴AD⊥面DEF;
又AD?面ABCD,∴面DEF⊥面ABCD;
证法二:设CM∩DE=O,连FO,∴O为MC的中点;
在△PMC中,FO∥PM,
∵PM⊥面ABCD,∴FO⊥面ABCD,
又FO?面DEF,∴面DEF⊥面ABCD.
 解:(1)如图
解:(1)如图过P作PM⊥AD于M,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PM?平面PAD,
∴PM⊥面ABCD;
又PA=PD=5,AD=8
∴M为AD的中点,且PM=
| 52-42 |
∵菱形ABCD中,∠BAD=
| π |
| 3 |
∴VP-ABCD=
| 1 |
| 3 |
| π |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 3 |
∴四棱锥P-ABCD的体积为32
| 3 |
(2)证明:连接BM,BD;
∵BD=BA=8,AM=DM,∠BAD=
| π |
| 3 |
又AD⊥PM,且BM∩PM=M,
∴AD⊥平面PMB,
∵PB?平面PMB,
∴AD⊥PB;
(3)能找到,并且点F为棱PC的中点,
证法一:∵F为PC的中点,点E为BC的中点,∴EF∥PB;
又由(2)可知AD⊥PB,∴AD⊥EF,
由AD⊥BM,BM∥DE,∴AD⊥DE;
又AD⊥EF,且DE∩EF=E,∴AD⊥面DEF;
又AD?面ABCD,∴面DEF⊥面ABCD;
证法二:设CM∩DE=O,连FO,∴O为MC的中点;
在△PMC中,FO∥PM,
∵PM⊥面ABCD,∴FO⊥面ABCD,
又FO?面DEF,∴面DEF⊥面ABCD.
点评:本题考查了求棱锥的体积与空间中的线线垂直,线面垂直,面面垂直的性质与判定,是易错题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
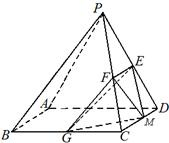 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.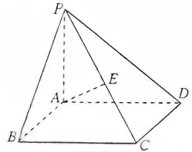 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2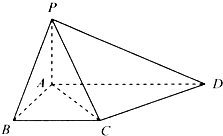 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.