题目内容
(2012•贵州模拟)在△ABC中,AB=3,AC=5,BC=7,角A的平分线交BC于E点.
(Ⅰ)求角A的大小;
(Ⅱ)设线段AE与EC长度分别为m、n,求
.
(Ⅰ)求角A的大小;
(Ⅱ)设线段AE与EC长度分别为m、n,求
| m | n |
分析:(Ⅰ)利用余弦定理表示出cosA,将已知的三边长代入求出cosA的值,由A为三角形的内角,利用特殊角的三角函数值即可求出A的度数;
(Ⅱ)由由AE为∠BAC的平分线,根据∠BAC的度数求出∠CAE的度数,在三角形ABC中,利用余弦定理表示出cosC,将三边长代入求出cosC的值,再利用同角三角函数间的基本关系求出sinC的值,在三角形ACE中,由AE=m,EC=n,sinC及sin∠CAE的值,利用正弦定理即可求出m与n的比值.
(Ⅱ)由由AE为∠BAC的平分线,根据∠BAC的度数求出∠CAE的度数,在三角形ABC中,利用余弦定理表示出cosC,将三边长代入求出cosC的值,再利用同角三角函数间的基本关系求出sinC的值,在三角形ACE中,由AE=m,EC=n,sinC及sin∠CAE的值,利用正弦定理即可求出m与n的比值.
解答: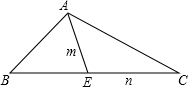 解:(Ⅰ)∵AB=c=3,AC=b=5,BC=a=7,
解:(Ⅰ)∵AB=c=3,AC=b=5,BC=a=7,
∴由余弦定理得:cosA=
=
=-
,
又A为三角形的内角,
则A=
;
(Ⅱ)由AE为∠BAC的平分线及(1)知:∠CAE=
,
在△ABC中,由余弦定理得:cosC=
=
,
∴sinC=
=
,
在△CAE中,由正弦定理得:
=
=
.
 解:(Ⅰ)∵AB=c=3,AC=b=5,BC=a=7,
解:(Ⅰ)∵AB=c=3,AC=b=5,BC=a=7,∴由余弦定理得:cosA=
| b2+c2-a2 |
| 2bc |
| 32+52-72 |
| 2×3×5 |
| 1 |
| 2 |
又A为三角形的内角,
则A=
| 2π |
| 3 |
(Ⅱ)由AE为∠BAC的平分线及(1)知:∠CAE=
| π |
| 3 |
在△ABC中,由余弦定理得:cosC=
| a2+b2-c2 |
| 2ab |
| 13 |
| 14 |
∴sinC=
| 1-cos2C |
3
| ||
| 14 |
在△CAE中,由正弦定理得:
| m |
| n |
| sinC | ||
sin
|
| 3 |
| 7 |
点评:此题属于解三角形的题型,涉及的知识有:正弦、余弦定理,同角三角函数间的基本关系,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目