题目内容
下列说法错误的是( )
分析:A.根据函数奇偶性的定义进行判断.B.根据充分条件和必要条件的定义判断.C.根据含有量词的命题的否定进行判断.D.根据等差数列的性质以及三角形的边角关系进行判断.
解答:解:A.∵f(-x)=ex+e-x=f(x),∴f(x)是偶函数,∴A错误.
B.若
•
>0,则cosθ=
>0,若cosθ=1,则θ=0时,满足条件,但此时0不是锐角,
若θ为锐角,则cosθ=
>0,即
•
>0,∴“
•
>0”是“θ为锐角”的必要非充分条件,正确.
C.特称命题的否定是全称命题,∴¬p:?x∈R,x2-x+1≠0,∴C正确.
D.若a、b、c等差数列,则b=
,由余弦定理得cosB=
=
=
≥
=
=
.
因此0<B≤
.∴D正确.
故选:A.
B.若
| a |
| b |
| ||||
|
|
若θ为锐角,则cosθ=
| ||||
|
|
| a |
| b |
| a |
| b |
C.特称命题的否定是全称命题,∴¬p:?x∈R,x2-x+1≠0,∴C正确.
D.若a、b、c等差数列,则b=
| a+c |
| 2 |
| a2+c2-b2 |
| 2ac |
a2+c2-(
| ||
| 2ac |
| 3a2+3c2-2ac |
| 8ac |
| 3×2ac-2ac |
| 8ac |
| 4ac |
| 8ac |
| 1 |
| 2 |
因此0<B≤
| π |
| 3 |
故选:A.
点评:本题主要考查各种命题的真假判断,涉及的知识点较多,综合性较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
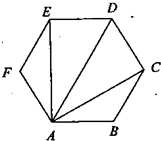 在正六边形ABCDEF中(如图),下列说法错误的是( )
在正六边形ABCDEF中(如图),下列说法错误的是( )