题目内容
【题目】如图,在四棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 且
且![]() ,
, ![]() 分别为
分别为![]() 的中点.
的中点.
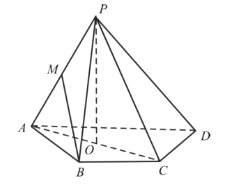
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)若二面角![]() 的大小为
的大小为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2) 见解析(3)![]()
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,根据题意易证四边形
,根据题意易证四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,从而易证结论;(2)由
,从而易证结论;(2)由![]() ,
, ![]() 可得线面垂直;(3)由二面角
可得线面垂直;(3)由二面角![]() 的大小为
的大小为![]() ,可得
,可得![]() ,求出底面直角梯形的面积,进而可得四棱锥
,求出底面直角梯形的面积,进而可得四棱锥![]() 的体积.
的体积.
试题解析:
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵![]() 为
为![]() 中点,∴
中点,∴![]() ,由已知
,由已知![]() ,
,
∴![]() ,∴四边形
,∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() .又
.又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)连接![]() ,∵
,∵![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]()
又![]() ,
, ![]() 为
为![]() 中点,∴
中点,∴![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() 平面
平面![]() .
.
(3)取![]() 的中点
的中点![]() ,连接
,连接![]() .∴
.∴![]() ,
, ![]() ,
,
∵![]() ,∴
,∴![]() ,又
,又![]() ,
, ![]() 为
为![]() 的中点,
的中点,
∴![]() ,故
,故![]() 为二面角
为二面角![]() 的平面角.
的平面角.
∴![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
由已知,四边形![]() 为直角梯形,∴
为直角梯形,∴![]() ,
,
∴![]()
![]() .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
【题目】某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价为5元,销售单价与日均销售量的关系如图所示.
销售单价/元 | … | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | … |
日均销售量/桶 | … | 480 | 460 | 440 | 420 | 400 | 380 | … |
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?