题目内容
(1)已知n∈N*,求证:1+2+22+23+…+25n-1能被31整除;
(2)求0.9986的近似值,使误差小于0.001.
(2)求0.9986的近似值,使误差小于0.001.
(1) 证明略(2) 0.9986≈1-0.012=0.988
(1)证明 ∵1+2+22+23+…+25n-1
=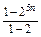 =25n-1=32n-1 3分
=25n-1=32n-1 3分
=(31+1)n-1
=31n+C ·31n-1+C
·31n-1+C ·31n-2+…+C
·31n-2+…+C ·31+1-1
·31+1-1
=31(31n-1+C ·31n-2+…+C
·31n-2+…+C ) 6分
) 6分
显然括号内的数为正整数,
故原式能被31整除. 7分
(2)解 ∵0.9986=(1-0.002)6
=1-C (0.002)+C
(0.002)+C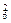 (0.002)2-C
(0.002)2-C (0.002)3+… 10分
(0.002)3+… 10分
第三项T3=15×(0.002)2="0.000" 06<0.001,以后各项更小,∴0.9986≈1-0.012="0.988. " 14分
=
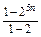 =25n-1=32n-1 3分
=25n-1=32n-1 3分=(31+1)n-1
=31n+C
 ·31n-1+C
·31n-1+C ·31n-2+…+C
·31n-2+…+C ·31+1-1
·31+1-1=31(31n-1+C
 ·31n-2+…+C
·31n-2+…+C ) 6分
) 6分显然括号内的数为正整数,
故原式能被31整除. 7分
(2)解 ∵0.9986=(1-0.002)6
=1-C
 (0.002)+C
(0.002)+C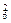 (0.002)2-C
(0.002)2-C (0.002)3+… 10分
(0.002)3+… 10分第三项T3=15×(0.002)2="0.000" 06<0.001,以后各项更小,∴0.9986≈1-0.012="0.988. " 14分

练习册系列答案
相关题目
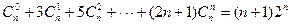
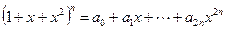 ,求
,求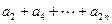 的值( )
的值( )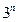
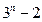
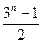
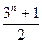
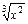 +3x2)n展开式中各项的系数和比各项的二项式系数和大992.求展开式中系数最大的项.
+3x2)n展开式中各项的系数和比各项的二项式系数和大992.求展开式中系数最大的项.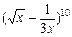 的展开式中含
的展开式中含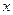 的正整数指数幂的项数是(
的正整数指数幂的项数是( )
)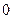
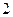
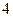

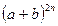 的二项展开式的项数是( )
的二项展开式的项数是( )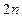
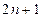
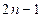
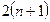
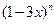
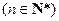 的展开式中所有项的系数之和为
的展开式中所有项的系数之和为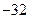 ,则
,则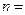 ( )
( )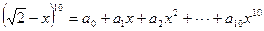 ,则
,则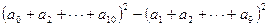 的值为( )
的值为( )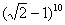
 的展开式中,
的展开式中, 的系数为______________.
的系数为______________.