题目内容
已知三棱锥 的所有顶点都在以
的所有顶点都在以 为球心的球面上,
为球心的球面上, 是边长为
是边长为 的正三角形,
的正三角形, 为球
为球 的直径,若三棱锥
的直径,若三棱锥 的体积为
的体积为 ,则球
,则球 的表面积为 .
的表面积为 .
 的所有顶点都在以
的所有顶点都在以 为球心的球面上,
为球心的球面上, 是边长为
是边长为 的正三角形,
的正三角形, 为球
为球 的直径,若三棱锥
的直径,若三棱锥 的体积为
的体积为 ,则球
,则球 的表面积为 .
的表面积为 .
试题分析:因为
 是边长为
是边长为 的正三角形,设
的正三角形,设 外接圆的半径为r,则可以求出
外接圆的半径为r,则可以求出 ,易知
,易知 是
是 的中点,它到四个顶点的距离相等,设球的半径为R,则点O到底面的距离为
的中点,它到四个顶点的距离相等,设球的半径为R,则点O到底面的距离为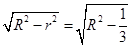 ,因为三棱锥
,因为三棱锥 的体积为
的体积为 ,
,所以
 ,所以球的表面积为
,所以球的表面积为 .
.点评:解决本小题的关键是求出球的球心位置,根据三棱锥的体积进而想办法求出球的半径.

练习册系列答案
相关题目









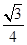 a2
a2 a2
a2 a2
a2 a2
a2 中,
中, 是棱
是棱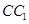 的中点,
的中点, 是侧面
是侧面 内的动点,且
内的动点,且 平面
平面 ,则
,则 与平面
与平面




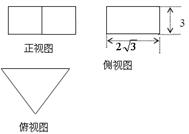
 ) cm2
) cm2 cm2
cm2  cm2
cm2 cm
cm 中,点
中,点 分别是
分别是 的中点,则下面四个结论不成立的是( )
的中点,则下面四个结论不成立的是( )




 平面PBD;
平面PBD;