题目内容
直线 与抛物线y2=4x相交于A、B两点,与x轴相交于点F,若
与抛物线y2=4x相交于A、B两点,与x轴相交于点F,若 ,则
,则 = .
= .
【答案】分析:直线过抛物线的焦点F(1,0),把直线方程代入抛物线的方程解得A、B 的坐标,由 得
得
到2 λ-
λ- μ=0,从而求得
μ=0,从而求得  的值.
的值.
解答:解:直线 过抛物线的焦点F(1,0),把直线方程代入抛物线的方程解得
过抛物线的焦点F(1,0),把直线方程代入抛物线的方程解得
 ,或
,或  ,不妨设A(3,2
,不妨设A(3,2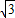 )、B (
)、B ( ,-
,- ).
).
∵ ,∴(1,0)=(3λ,2
,∴(1,0)=(3λ,2 λ)+(
λ)+( μ,-
μ,- μ)
μ)
=(3λ+ μ,2
μ,2 λ-
λ- μ ).
μ ).
∴3λ+ μ=1,2
μ=1,2 λ-
λ-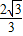 μ=0,λ≤μ.∴
μ=0,λ≤μ.∴ =
= ,
,
故答案为 .
.
点评:本题考查两个向量坐标形式的运算,直线和抛物线的位置关系,由 得到2
得到2 λ-
λ- μ=0,
μ=0,
是解题的关键.
 得
得到2
 λ-
λ- μ=0,从而求得
μ=0,从而求得  的值.
的值.解答:解:直线
 过抛物线的焦点F(1,0),把直线方程代入抛物线的方程解得
过抛物线的焦点F(1,0),把直线方程代入抛物线的方程解得 ,或
,或  ,不妨设A(3,2
,不妨设A(3,2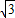 )、B (
)、B ( ,-
,- ).
).∵
 ,∴(1,0)=(3λ,2
,∴(1,0)=(3λ,2 λ)+(
λ)+( μ,-
μ,- μ)
μ) =(3λ+
 μ,2
μ,2 λ-
λ- μ ).
μ ).∴3λ+
 μ=1,2
μ=1,2 λ-
λ-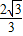 μ=0,λ≤μ.∴
μ=0,λ≤μ.∴ =
= ,
,故答案为
 .
.点评:本题考查两个向量坐标形式的运算,直线和抛物线的位置关系,由
 得到2
得到2 λ-
λ- μ=0,
μ=0,是解题的关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目