题目内容
过点(0,4),斜率为-1的直线与抛物线y2=2px(p>0)交于两点A、B,且弦|AB|的长度为4
.
(1)求p的值;
(2)求证:OA⊥OB(O为原点).
| 10 |
(1)求p的值;
(2)求证:OA⊥OB(O为原点).
分析:(1)联立直线与抛物线方程,利用韦达定理,计算弦|AB|的长度,即可求p的值;
(2)证明x1x2+y1y2=0,即可得到OA⊥OB.
(2)证明x1x2+y1y2=0,即可得到OA⊥OB.
解答:(1)解:直线方程为y=-x+4,联立方程
消去y得,x2-2(p+4)x+16=0.
设A(x1,y1),B(x2,y2),得x1+x2=2(p+4),x1x2=16,△=4(p+2)2-64>0.
所以|AB|=
|x1-x2|=
•
=4
,所以p=2.
(2)证明:由(1)知,x1+x2=2(p+4)=12,x1x2=16,
∴y1y2=(-x1+4)(-x2+4)=-8p=-16
∴x1x2+y1y2=0,∴OA⊥OB.
|
设A(x1,y1),B(x2,y2),得x1+x2=2(p+4),x1x2=16,△=4(p+2)2-64>0.
所以|AB|=
| 1+1 |
| 2 |
| 4(P+4)2-4×16 |
| 10 |
(2)证明:由(1)知,x1+x2=2(p+4)=12,x1x2=16,
∴y1y2=(-x1+4)(-x2+4)=-8p=-16
∴x1x2+y1y2=0,∴OA⊥OB.
点评:本题考查直线与抛物线的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 交于两点A,B,如果
交于两点A,B,如果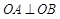 (O为原点)求P的值及抛物线的焦点坐标.
(O为原点)求P的值及抛物线的焦点坐标. .
.