题目内容

8．函数f（x）=$\frac{1}{x}$在区间[3，5]上值域为[$\frac{1}{5}$，$\frac{1}{3}$]．

分析 先分析函数f（x）=$\frac{1}{x}$在区间[3，5]上的单调性，进而求出函数f（x）=$\frac{1}{x}$在区间[3，5]上的最值，可得答案．

解答 解：函数f（x）=$\frac{1}{x}$在区间[3，5]上为减函数，
由f（3）=$\frac{1}{3}$，f（5）=$\frac{1}{5}$，
可得函数f（x）=$\frac{1}{x}$在区间[3，5]上值域为[$\frac{1}{5}$，$\frac{1}{3}$]，
故答案为：[$\frac{1}{5}$，$\frac{1}{3}$]

点评 本题考查的知识点是反比例函数的图象和性质，函数的值域，难度中档．

练习册系列答案
相关题目
16．{$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$}构成空间中的一个基底，$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$=$\frac{{z}_{1}}{{z}_{2}}$是$\overrightarrow{p}$=x1$\overrightarrow{a}$+y1$\overrightarrow{b}$+z1$\overrightarrow{c}$与$\overrightarrow{q}$=x2$\overrightarrow{a}$+y2$\overrightarrow{b}$+z2$\overrightarrow{c}$共线的充分不必要条件．
19．若函数$f（x）={log_{a+2}}（a{x^2}-3x+2）$的值域为R，则a的取值范围是$[0，\frac{9}{8}]$．
16．如图是偶函数y=f（x）的局部图象，根据图象所给信息，下列结论正确的是（　　）
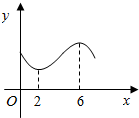
A．f（-2）-f（6）=0B．f（-2）-f（6）＜0C．f（-2）+f（6）=0D．f（-2）-f（6）＞0
3．直线l：x-y+2=0过椭圆的左焦点F1和一个顶点B，该椭圆的离心率为$\frac{\sqrt{2}}{2}$．
13．设P和Q是两个集合，定义集合P+Q={x∈P或x∈Q且∉P∩Q}，若P={x|x2-3x-4≤0}，Q={x|y=log2（x2-2x-15）}，那么P+Q等于（　　）
A．[-1，4]B．（-∞，-1]∪[4，+∞）C．（-3，5）D．（-∞，-3）∪[-1，4]∪（5，+∞）
20．已知椭圆的中心在坐标原点O，焦点在x轴上，椭圆的短轴端点和焦点所组成的四边形为正方形，且焦距为4．
（1）求椭圆的方程；
（2）直线l过点P（0，2）且与椭圆相交于A、B两点，当△AOB面积取得最大值时，求直线l的方程．
17．设定义域为R的函数f（x）=$\left\{\begin{array}{l}{\frac{1}{|x-1|}（x≠1）}\\{1（x=1）}\end{array}\right.$，若关于x的方程f2（x）+bf（x）+c=0有5个不同的实数解，则b+c值为（　　）
A．0B．1C．-1D．不能确定
18．已知函数$f（x）=\frac{{{2^x}-1}}{{{2^x}+1}}$的定义域为[-3，3]．
（1）判断函数f（x）的单调性，并用定义给出证明；
（2）若实数m满足f（m-1）＜f（1-2m），求m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网