题目内容
（2013•广元一模）如图所示，AF、DE分别是⊙O和⊙O1的直径，AD与两圆所在平面都垂直，AD=8，BC是⊙O的直径，AB=AC=6，OE∥AD．①求二面角 B-AD-F 的大小；
②求异面直线BD与EF所成的角的正弦值．
分析：（1）先证明平面角∠BAF的大小为二面角B-AD-F的大小，再计算其大小即可；
（2）先证明∠BDO为直线BD与EF所成的角，再在Rt△BDO中计算即可．
（2）先证明∠BDO为直线BD与EF所成的角，再在Rt△BDO中计算即可．
解答：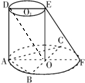
解：（1）∵AD⊥底面ABFC，∴DA⊥AB，DA⊥AF，
∴平面角∠BAF的大小为二面角B-AD-F的大小，
∵AB=AC=6，∴△ABC为等腰直角三角形，BA⊥AC，
又O为AC中点，∴∠BAF=45°，
∴二面角B-AD-F的大小为45°；
（2）∵OE∥AD，DE∥AO，∴四边形DAOE为矩形，
∴DE∥AO，DE=AO，∴DE∥OF，DE=OF，
连结DO，∴DO∥EF，∴∠BDO为直线BD与EF所成的角．
∵BC⊥AO，∴BO⊥面DAO，∴BO⊥OD．
Rt△BDO中，BO=AO=3
，∴DO=
=
，∴BD=10
∴sinn∠BDO=
=
∴直线BD与EF所成的角的正弦值为
．
解：（1）∵AD⊥底面ABFC，∴DA⊥AB，DA⊥AF，∴平面角∠BAF的大小为二面角B-AD-F的大小，
∵AB=AC=6，∴△ABC为等腰直角三角形，BA⊥AC，
又O为AC中点，∴∠BAF=45°，
∴二面角B-AD-F的大小为45°；
（2）∵OE∥AD，DE∥AO，∴四边形DAOE为矩形，
∴DE∥AO，DE=AO，∴DE∥OF，DE=OF，
连结DO，∴DO∥EF，∴∠BDO为直线BD与EF所成的角．
∵BC⊥AO，∴BO⊥面DAO，∴BO⊥OD．
Rt△BDO中，BO=AO=3
| 2 |
| AD2+AO2 |
| 82 |
∴sinn∠BDO=
| BO |
| BD |
3
| ||
| 10 |
∴直线BD与EF所成的角的正弦值为
3
| ||
| 10 |
点评：本题考查面面角，考查异面直线所成角的计算，考查学生分析解决问题的能力，正确作出空间角是关键，
练习册系列答案
优等生题库系列答案
53天天练系列答案
相关题目