题目内容
已知P为圆x2+(y-1)2=1上任意一点,直线OP的倾斜角为θ弧度,O为坐标原点,记d=|OP|,以(θ,d)为坐标的点的轨迹为C,则曲线C与x轴围成的封闭图形的面积为分析:由题意可知,在OP与直径围成的三角形中通过解三角形求出d与θ的函数关系,再根据函数表达式作出图象,最后利用定积分表示出所求面积,解之即可.
解答: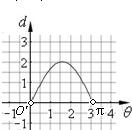 解:在直角三角形中,因直径的长度为2,其所邻的角为
解:在直角三角形中,因直径的长度为2,其所邻的角为
-θ故
|OP|=2cos(
-θ)=2sinθ,θ∈(0,π)
故函数图象为
曲线C与x轴围成的封闭图形的面积为∫0π2sinxdx=(-2cosx)|0π=2+2=4
故答案为:4
 解:在直角三角形中,因直径的长度为2,其所邻的角为
解:在直角三角形中,因直径的长度为2,其所邻的角为 | π |
| 2 |
|OP|=2cos(
| π |
| 2 |
故函数图象为
曲线C与x轴围成的封闭图形的面积为∫0π2sinxdx=(-2cosx)|0π=2+2=4
故答案为:4
点评:本题考点是直线与圆的位置关系,在圆中考查三角函数,是本题的一大亮点,新颖,同时考查了定积分的应用,属于中档题.

练习册系列答案
相关题目
