题目内容
已知函数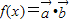 ,其中
,其中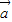 =(
=(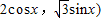 ,
,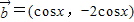
(1)求函数f(x)在[0,π]上的单调递增区间和最小值;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,且f(A)=-1,求
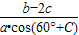 的值.
的值.
【答案】分析:计算向量的数量积,利用二倍角.两角和的正弦函数化简函数f(x)的表达式,得到一个角的一个三角函数的形式;
(1)借助正弦函数的单调增区间,求函数y=f(x)的单调递增区间.借助正弦函数的最值,求出函数y=f(x)的最小值,以及取得最小值时x的值;
(2)通过f(A)的表达式,可求得A的值,再利用正弦定理化简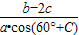 求出表达式的值.
求出表达式的值.
解答:解:(1)函数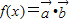 =
=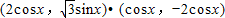
=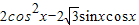 ,所以
,所以
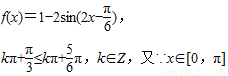
所以函数的单调增区间为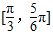
∴f(x)min=1-2=-1
(2)∵f(A)=-1,
∴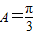
由正弦定理可知:
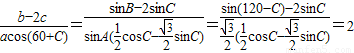 .
.
所以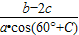 为2.
为2.
点评:本题主要考查二倍角公式、余弦定理和两角和与差的公式的应用.高考对三角函数的考查以基础题为主,但是这部分公式比较多不容易记忆,也为这一部分增加了难度;考查三角函数的单调性,三角函数的最值,考查计算能力,基本知识的灵活运应能力,考查转化思想.
(1)借助正弦函数的单调增区间,求函数y=f(x)的单调递增区间.借助正弦函数的最值,求出函数y=f(x)的最小值,以及取得最小值时x的值;
(2)通过f(A)的表达式,可求得A的值,再利用正弦定理化简
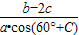 求出表达式的值.
求出表达式的值.解答:解:(1)函数
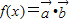 =
=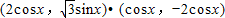
=
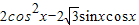 ,所以
,所以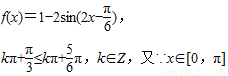
所以函数的单调增区间为
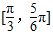
∴f(x)min=1-2=-1
(2)∵f(A)=-1,
∴
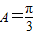
由正弦定理可知:
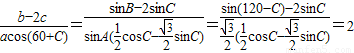 .
.所以
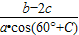 为2.
为2.点评:本题主要考查二倍角公式、余弦定理和两角和与差的公式的应用.高考对三角函数的考查以基础题为主,但是这部分公式比较多不容易记忆,也为这一部分增加了难度;考查三角函数的单调性,三角函数的最值,考查计算能力,基本知识的灵活运应能力,考查转化思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目






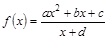 (其中
(其中 是实数常数,
是实数常数, )
) ,函数
,函数 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求 的值;
的值; ,总有
,总有 ,求
,求 的取值范围;
的取值范围; ,
, ,且对任意
,且对任意 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数 的取值范围.
的取值范围.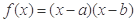 (其中
(其中 )的图象如图(上)所示,则函数
)的图象如图(上)所示,则函数 的图象是( )
的图象是( ) 
