题目内容
已知函数 ,其中
,其中 是自然对数的底数,
是自然对数的底数, .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)当 时,求函数
时,求函数 的最小值.
的最小值.
【答案】
(Ⅰ) 的单调减区间为
的单调减区间为 ;单调增区间为
;单调增区间为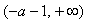 ;(Ⅱ)
;(Ⅱ)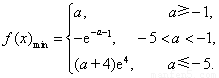
【解析】
试题分析:(Ⅰ)先求导函数,得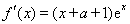 ,令
,令 ,得递增区间为
,得递增区间为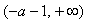 ;令
;令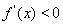 ,得递减区间为
,得递减区间为 ;(Ⅱ)令
;(Ⅱ)令 ,得
,得 ,讨论
,讨论 与区间
与区间 的位置关系,当
的位置关系,当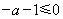 ,或
,或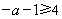 时,函数单调,利用单调性求最值;当
时,函数单调,利用单调性求最值;当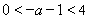 ,将定义域分段,分别判断导函数符号,得单调区间,判断函数的值图像,从而求得最值.
,将定义域分段,分别判断导函数符号,得单调区间,判断函数的值图像,从而求得最值.
试题解析:(Ⅰ)解:因为 ,
, ,所以
,所以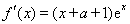 .
.
令 ,得
,得 .当
.当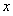 变化时,
变化时, 和
和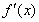 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
|
| ↘ |
| ↗ |
故 的单调减区间为
的单调减区间为 ;单调增区间为
;单调增区间为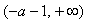 .
.
(Ⅱ)解:由(Ⅰ),得 的单调减区间为
的单调减区间为 ;单调增区间为
;单调增区间为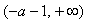 .
.
所以当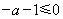 ,即
,即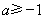 时,
时, 在
在 上单调递增,
上单调递增,
故 在
在 上的最小值为
上的最小值为 ;
;
当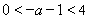 ,即
,即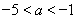 时,
时,
 在
在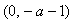 上单调递减,
上单调递减,  在
在 上单调递增,
上单调递增,
故 在
在 上的最小值为
上的最小值为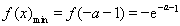 ;
;
当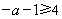 ,即
,即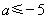 时,
时, 在
在 上单调递减,
上单调递减,
故 在
在 上的最小值为
上的最小值为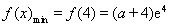 .
.
所以函数 在
在 上的最小值为
上的最小值为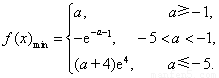
考点:1、导数在单调性上的应用;2、导数在极值、最值上的应用.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
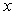
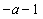
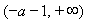

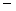
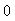
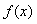
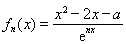
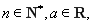
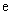
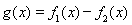


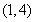

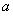
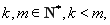
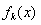
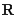
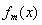
 ,其中
,其中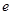 是自然对数的底数,
是自然对数的底数,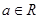 .
.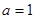 ,求曲线
,求曲线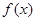 在点
在点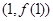 处的切线方程;
处的切线方程;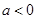 ,求
,求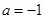 ,函数
,函数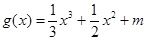 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数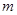 的取值范围.
的取值范围. 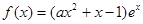 ,其中
,其中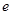 是自然对数的底数,
是自然对数的底数,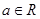 .
.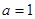 ,求曲线
,求曲线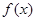 在点
在点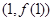 处的切线方程;
处的切线方程;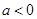 ,求
,求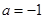 ,函数
,函数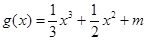 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数 的取值范围.
的取值范围.