题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 的极值点的个数;
的极值点的个数;
(2)若方程![]() 在
在![]() 上有且只有一个实根,求
上有且只有一个实根,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() 时,
时,![]() 有一个极值点;当
有一个极值点;当![]() 时,
时,![]() 有两个极值点.
有两个极值点.
(2) ![]() 或
或![]() 或
或![]()
【解析】
(1)对![]() 求导,讨论
求导,讨论![]() 的解是否在
的解是否在![]() ,在
,在![]() 时判断解左右的导数符号,确定极值点的个数.
时判断解左右的导数符号,确定极值点的个数.
(2)利用(1)所求,对a讨论,研究函数![]() 的单调性及极值,应用零点存在定理判断何时方程
的单调性及极值,应用零点存在定理判断何时方程![]() 在
在![]() 上有且只有一个实根.
上有且只有一个实根.
(1)![]() 的定义域为
的定义域为![]() ,
,![]() .
.
由![]() 得
得![]() 或
或![]() .
.
当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
在![]() 上单调递减,
上单调递减,![]() 在
在![]() 处取得极小值,无极大值;
处取得极小值,无极大值;
当![]() ,即
,即![]() 时,由
时,由![]() 得
得![]() ,或
,或![]() ,
,
由![]() 得
得![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() 在
在![]() 处取得极小值,在
处取得极小值,在![]() 处取得极大值.
处取得极大值.
综上,当![]() 时,
时,![]() 有一个极值点;当
有一个极值点;当![]() 时,
时,![]() 有两个极值点.
有两个极值点.
(2)当![]() 时,设
时,设![]() ,
,
则![]() 在
在![]() 上有且只有一个零点.
上有且只有一个零点.
显然函数![]() 与
与![]() 的单调性是一致的.
的单调性是一致的.
①当![]() 时,由(1)知函数
时,由(1)知函数![]() 在区间
在区间![]() 上递减,
上递减,![]() 上递增,
上递增,
所以![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
由于![]() ,要使
,要使![]() 在
在![]() 上有且只有一个零点,
上有且只有一个零点,
需满足![]() 或
或![]() ,解得
,解得![]() 或
或![]() .
.
②当![]() 时,因为函数
时,因为函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
∵![]() ,∴当
,∴当![]() 时,总有
时,总有![]() .
.
∵![]() ,
,
∴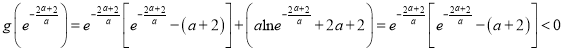 ,又
,又![]()
∴![]() 在
在![]() 上必有零点.
上必有零点.
∵![]() 在
在![]() 上单调递增,
上单调递增,
∴当![]() 时,
时,![]() 在
在![]() 上有且只有一个零点.
上有且只有一个零点.
综上,当![]() 或
或![]() 或
或![]() 时,方程
时,方程![]() 在
在![]() 上有且只有一个实根.
上有且只有一个实根.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目