Question

【题目】如图，在长方体ABCD﹣A1B1C1D1中，E是CD上一点，AB=AD=3，AA1=2，CE=1，P是AA1上一点，且DP∥平面AEB1 ， F是棱DD1与平面BEP的交点，则DF的长为（ ）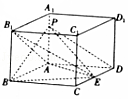
A.1
B.
C.
D.

Answer 1

【答案】B
【解析】解：在长方体ABCD﹣A1B1C1D1的棱AB上取点M，使得BM=1， 过点M作MN∥BB1 ， 交AB1于N，连接EM、EN，如图所示；
则平面EMN∥平面ADD1A1；
∵BB1=2AM=2BM，
∴MN= ，
∴当AP=MN= 时，DP∥EN，
即DP∥平面AEB；
∵F是棱DD1与平面BEP的交点，
∴EF∥BP；
取DG=AP= ，连接CG，则CG∥BP，
∴EF∥CG，
∴DF= DG= ．
故选：B．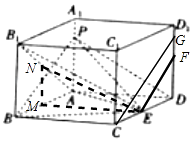

【考点精析】通过灵活运用棱柱的结构特征，掌握两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形即可以解答此题．