题目内容
已知函数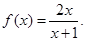
(1)当 时, 证明: 不等式
时, 证明: 不等式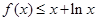 恒成立;
恒成立;
(2)若数列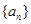 满足
满足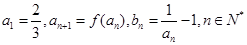 ,证明数列
,证明数列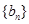 是等比数列,并求出数列
是等比数列,并求出数列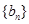 、
、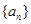 的通项公式;
的通项公式;
(3)在(2)的条件下,若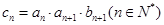 ,证明:
,证明: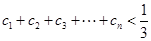 .
.
【答案】
(1)证明略
(2)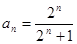 ,
,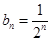 ,
,
(3)证明略
【解析】(1)方法一:∵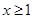 ,
,
∴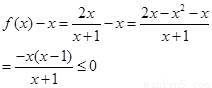
而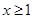 时,
时,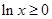 ,∴
,∴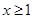 时,
时,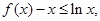
∴当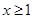 时,
时,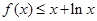 恒成立.
恒成立.
方法二:令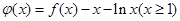 ,
,


故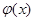 是定义域
是定义域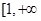 )上的减函数,
)上的减函数,
∴当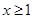 时,
时, 恒成立.
恒成立.
即当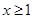 时,
时,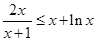 恒成立.
恒成立.
∴当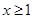 时,
时,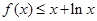 恒成立. ……4分
恒成立. ……4分
(2)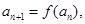 ∴
∴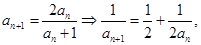
∵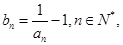 ∴
∴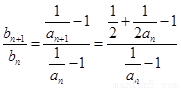
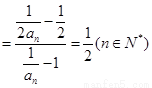 ,
,
又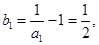
∴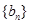 是首项为
是首项为 ,公比为
,公比为 的等比数列,其通项公式为
的等比数列,其通项公式为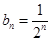 .
.
又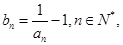
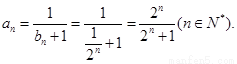 ……10分
……10分
(3) 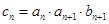
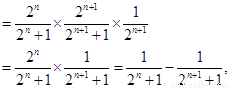 W$
W$

练习册系列答案
相关题目
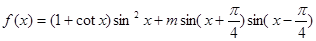 .
.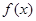 在区间
在区间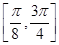 上的取值范围;
上的取值范围; 时,
时,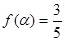 ,求m的值.
,求m的值.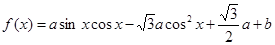
 〉0时,写出函数的单调递减区间;
〉0时,写出函数的单调递减区间;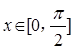 ,
,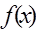 的最小值是
的最小值是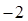 ,最大值是
,最大值是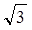 ,求实数
,求实数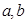 的值.
的值.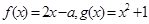 ,
,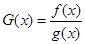 ,
,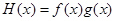 .
.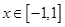 ,求使
,求使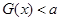 恒成立的
恒成立的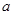 的取值范围;
的取值范围;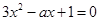 的两根为
的两根为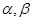 (
(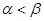 ),且函数
),且函数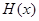 在区间
在区间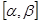 上的最大值与最小值之差是8,求
上的最大值与最小值之差是8,求