题目内容
已知函数![]() (1)当a=4,
(1)当a=4,![]() ,求函数f(x)的最大值;(2)若x≥a , 试求f(x)+3 >0 的解集;(3)当
,求函数f(x)的最大值;(2)若x≥a , 试求f(x)+3 >0 的解集;(3)当![]() 时,f(x)≤2x – 2 恒成立,求实数a的取值范围.
时,f(x)≤2x – 2 恒成立,求实数a的取值范围.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]() (Ⅲ)
(Ⅲ)![]()
解析:
:(1)当![]() 时,
时,![]() ,
,
①![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
![]() …2分
…2分
②当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
![]() 综上所述,当
综上所述,当![]() 时,
时,![]()
![]() … 4分
… 4分
(2)若![]() ,
, ![]() ,………6分
,………6分
当![]() 时,
时,![]() ,或
,或![]() ,因为
,因为![]() ,所以
,所以![]() ;
;
当![]() ,所以
,所以![]() ; 当
; 当![]() 时,
时,![]() ,或
,或![]() , ①若
, ①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]()
![]() 综上可知:当
综上可知:当![]() 时,所求不等式的解集为
时,所求不等式的解集为![]() ;……10分当
;……10分当![]() 时,所求不等式的解集为
时,所求不等式的解集为![]()
![]() ………12分
………12分
(3)方法1:当![]() 时,
时,![]()
即![]()
![]()
![]()
![]() ……14分
……14分
因为![]() 在
在![]() 上增,最大值是
上增,最大值是![]() ,
,
![]() 在
在![]() 上增,最小值是
上增,最小值是![]() ,故只需
,故只需![]() .…16分
.…16分
方法2:若![]() ,原不等式可化为
,原不等式可化为![]() ,即
,即![]() 在
在![]() 上恒成立,
上恒成立,![]()
![]() …13分若
…13分若![]() ,原不等式可化为:
,原不等式可化为:![]() ,
,
所以![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() .……15分
.……15分
综上可知![]() 的取值范围是
的取值范围是![]()
![]() ………16分
………16分

练习册系列答案
相关题目
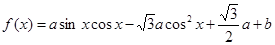
 〉0时,写出函数的单调递减区间;
〉0时,写出函数的单调递减区间;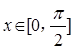 ,
,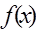 的最小值是
的最小值是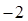 ,最大值是
,最大值是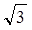 ,求实数
,求实数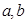 的值.
的值.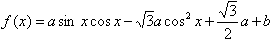
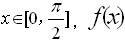 的最小值是-2,最大值是
的最小值是-2,最大值是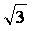 ,求实数
,求实数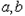 的值.
的值.