题目内容
【题目】已知某椭圆C,它的中心在坐标原点,左焦点为F(﹣![]() ,0),且过点D(2,0).
,0),且过点D(2,0).
(1)求椭圆C的标准方程;
(2)若已知点A(1,![]() ),当点P在椭圆C上变动时,求出线段PA中点M的轨迹方程.
),当点P在椭圆C上变动时,求出线段PA中点M的轨迹方程.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
试题(1)根据题意椭圆的焦点在x轴上,a=2且c=![]() ,从而b=1,得到椭圆的标准方程;
,从而b=1,得到椭圆的标准方程;
(2)设点P(x0,y0),线段PA的中点为M(x,y),根据中点坐标公式将x0、y0表示成关于x、y的式子,将P(x0,y0)关于x、y的坐标形式代入已知椭圆的方程,化简整理即可得到线段PA的中点M的轨迹方程.
解:(1)由题意知椭圆的焦点在x轴上,
∵椭圆经过点D(2,0),左焦点为F(﹣![]() ,0),
,0),
∴a=2,c=![]() ,可得b=1
,可得b=1
因此,椭圆的标准方程为![]() .
.
(2)设点P的坐标是(x0,y0),线段PA的中点为M(x,y),
由根据中点坐标公式,可得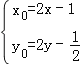 ,
,
∵点P(x0,y0)在椭圆上,
∴可得![]() ,化简整理得
,化简整理得![]() ,
,
∴线段PA中点M的轨迹方程是![]() .
.

练习册系列答案
相关题目