题目内容
【题目】对于函数f(x)，若存在x0∈R，使得f(x0)=x0成立，则称x0为f(x)的天宫一号点.已知函数f(x)=ax2+(b-7)x+18的两个天宫一号点分别是-3和2.
(1)求a,b的值及f(x)的表达式；
(2)当函数f(x)的定义域是［t,t+1］时，求函数f(x)的最大值g(t).
【答案】（1）f(x)=-3x2-2x+18；（2）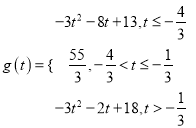
.
【解析】试题分析：（1）依题意得f(-3)=-3,f(2)=2，带入解方程即可；
（2）比较函数对称轴
和定义域［t,t+1］的位置关系，依次得最大值.
试题解析：
(1)依题意得f(-3)=-3,f(2)=2，即
解得
∴f(x)=-3x2-2x+18.
(2)①当区间［t,t+1］在对称轴
左侧时,即
,也即
时，
f(x)的最大值为f(t+1)=-3t2-8t+13；
②当对称轴
在［t,t+1］内时,即
,也即
时,
f(x)的最大值为
；
③当［t,t+1］在
右侧时,即
时，
f(x)的最大值为f(t)=-3t2-2t+18，
所以g(t)=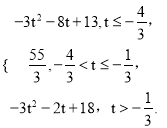 
练习册系列答案
相关题目
