题目内容
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(Ⅰ)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为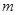 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为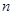 ,求
,求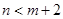 的概率.
的概率.
(Ⅰ)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为
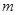 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为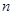 ,求
,求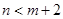 的概率.
的概率.(Ⅰ) 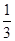 ; (Ⅱ)
; (Ⅱ) 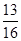 .
.
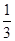 ; (Ⅱ)
; (Ⅱ) 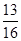 .
.试题分析:本题两问中,一个是无放回取球,一个是有放回取球,试题通过这两个问题,考查列举基本事件个数、找出所求的随机事件所含有的基本事件个数的数据处理能力以及运算求解能力.(Ⅰ)四个球中不放回取出两个球,取出的球的编号之和不大于4的概率 ,列举基本事件的个数,从中找出随机事件“球的编号之和不大于4”所包含的基本事件的个数,根据古典概型的公式进行计算;(Ⅱ)有放回地从四个球中取出两个球,求解一个古典概型,仍然是列举基本事件的个数,再从中找出随机事件“
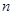
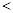
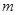 +2”所含有的基本事件的个数,根据古典概型的公式进行计算.
+2”所含有的基本事件的个数,根据古典概型的公式进行计算.试题解析:(Ⅰ)从袋子中随机取两个球,其一切可能的结果组成的基本事件有
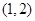 ,
,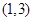 ,
,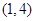 ,
,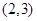 ,
,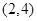 ,
,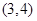 共6个. 3分
共6个. 3分从袋中随机取出的球的编号之和不大于4的事件共有
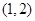 ,
,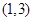 ,有两个.因此所求事件的概率为
,有两个.因此所求事件的概率为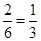 . 6分
. 6分(Ⅱ)先从袋中随机取一个球,记下编号为
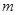 ,放回后,再从袋中随机取一个球,记下编号为
,放回后,再从袋中随机取一个球,记下编号为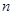 ,其一切可能的结果
,其一切可能的结果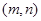 有:(1,1),
有:(1,1),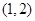 ,
,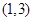 ,
,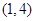 ,
,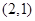 ,
,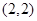 ,
,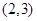 ,
,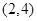 ,
,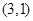 ,
,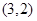 ,
,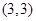 ,
,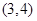 ,
,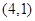 ,
,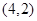 ,
,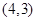 ,
,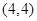 ,共16个. 9分
,共16个. 9分满足条件
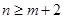 的事件为
的事件为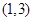 ,
,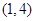 ,
,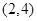 共3个,所以满足条件
共3个,所以满足条件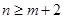 的事件的概率
的事件的概率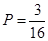 ,
,故满足条件
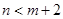 的事件的概率为
的事件的概率为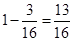 . 12分
. 12分
练习册系列答案
相关题目
 关于
关于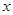 的线性回归方程
的线性回归方程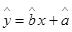 ,
,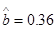
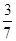 ,
,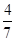 .
.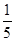 ;采用3期付款的只能改为2期,概率为
;采用3期付款的只能改为2期,概率为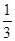 .数码城销售一台该平板电脑,实际付款期数
.数码城销售一台该平板电脑,实际付款期数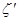 与利润
与利润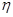 (元)的关系为
(元)的关系为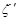
 ,
, ,若向区域
,若向区域 上随机投一点
上随机投一点 ,则点
,则点 的概率为____________。
的概率为____________。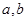 ,使得
,使得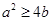 的概率是( )
的概率是( )
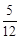

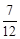
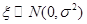 ,若
,若 ,则
,则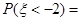 .
.