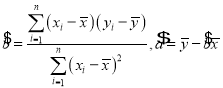题目内容
【题目】某运动会将在深圳举行，组委会招募了12名男志愿者和18名女志愿者，将这30名志愿者的身高编成如图所示的茎叶图（单位：
），身高在
以上（包括）定义为“高个子”，身高在以下（不包括）定义为“非高个子”．
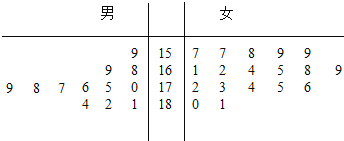
（1）如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人，再从这5人中选2人，求至少有一人是“高个子”的概率；
（2）若从身高
以上（包括）的志愿者中选出男、女各一人，设这2人身高相差
（
），求
的分布列和数学期望（均值）．
【答案】（1）
；（2）分布列见解析，
【解析】
（1）根据分层抽样的比例关系得到人数，再计算概率得到答案.
（2）
的可能取值为
，计算概率得到分布列，再计算数列期望得到答案.
（1）根据茎叶图：“高个子”有
个，“非高个子”有
个，
故抽取的“高个子”为
个，抽取的“非高个子”有
个.
至少有一人是“高个子”的概率为
.
（2）身高
以上（包括）的志愿者中选出男，女各有3人和2人，
故的可能取值为，
故
，
， 
，
，
.
故分布列为：
|
|
|
|
|
|
|
|
|
|
|
|
故
.
练习册系列答案
相关题目
【题目】为了解某地区足球特色学校的发展状况，某调查机构得到如下统计数据：
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校y（百个） | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
（1）根据上表数据，计算y与x的相关系数r，并说明y与x的线性相关性强弱（已知：
则认为
与
线性相关性很强；
，则认为与线性相关性一般，
，则认为y与x线性相关性较弱）
（2）求y与x的线性回归方程，并预测该地区2019年足球特色学校的个数（精确到个位）
参考公式：
；
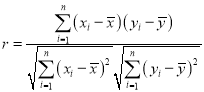
