题目内容
给出下列五个命题:
①长度相等,方向不同的向量叫做相反向量;
②设 ,
, 是同一平面内的两个不共线向量,则对于平面内的任意一个向量
是同一平面内的两个不共线向量,则对于平面内的任意一个向量 ,有且只有一对实数λ1,λ2,使
,有且只有一对实数λ1,λ2,使 =λ1
=λ1 +λ2
+λ2 ;
;
③ ∥
∥ 的充要条件是存在唯一的实数λ使
的充要条件是存在唯一的实数λ使 =λ
=λ ;
;
④( •
• )
) =
= (
( •
• );
);
⑤λ( +
+ )•
)• =λ
=λ •
• +λ
+λ •
• .
.
其中正确命题的个数是
- A.2
- B.3
- C.4
- D.其它
A
分析:由相反向量的定义可判断①的真假,由平面向量基本定理可判断②的真假,由向量共线的充要条件可判断③的真假,由向量数量积运算的运算律可判断④的真假,由向量的数量积运算分配律及实数与向量积的运算性质可判断⑤的真假
解答:①长度相等,方向相反的向量叫做相反向量,故①错误
②由平面向量基本定理可知②正确
③若 =
= ,则λ不唯一,故③错误
,则λ不唯一,故③错误
④若 ,
,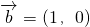 ,
, ,则(
,则( •
• )
) =
= ,
, (
( •
• )=
)= ,∴(
,∴( •
• )
) ≠
≠ (
( •
• ),故④错误;
),故④错误;
⑤由向量的数量积运算性质及实数与向量积的运算性质知⑤正确
故正确命题为②⑤
故选A
点评:本题考查了平面向量的相关概念,平面向量基本定理,向量共线的充要条件,向量数量积运算的运算律等基础知识
分析:由相反向量的定义可判断①的真假,由平面向量基本定理可判断②的真假,由向量共线的充要条件可判断③的真假,由向量数量积运算的运算律可判断④的真假,由向量的数量积运算分配律及实数与向量积的运算性质可判断⑤的真假
解答:①长度相等,方向相反的向量叫做相反向量,故①错误
②由平面向量基本定理可知②正确
③若
 =
= ,则λ不唯一,故③错误
,则λ不唯一,故③错误④若
 ,
,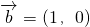 ,
, ,则(
,则( •
• )
) =
= ,
, (
( •
• )=
)= ,∴(
,∴( •
• )
) ≠
≠ (
( •
• ),故④错误;
),故④错误;⑤由向量的数量积运算性质及实数与向量积的运算性质知⑤正确
故正确命题为②⑤
故选A
点评:本题考查了平面向量的相关概念,平面向量基本定理,向量共线的充要条件,向量数量积运算的运算律等基础知识

练习册系列答案
相关题目