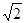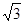题目内容
(5分)(2011•重庆)若△ABC的内角A,B,C满足6sinA=4sinB=3sinC,则cosB=( )
A.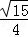 | B.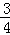 | C.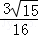 | D.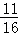 |
D
试题分析:由题意利用正弦定理,推出a,b,c的关系,然后利用余弦定理求出cosB的值.
解:△ABC的内角A,B,C满足6sinA=4sinB=3sinC,所以6a=4b=3c,不妨令a=2,b=3,c=4,
所以由余弦定理:b2=a2+c2﹣2accosB,所以cosB=
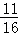 ,
,故选D.
点评:本题是基础题,考查正弦定理,余弦定理的应用,考查计算能力,常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 sinA-cos(B+
sinA-cos(B+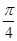 )的最大值为( )
)的最大值为( )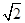
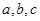 分别为角A、B、C所对的边,已知
分别为角A、B、C所对的边,已知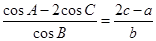 ,
,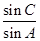 的值;
的值; 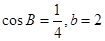 ,求△ABC的面积.
,求△ABC的面积.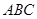 中,
中,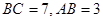 ,且
,且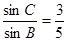 .
.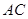 ; (2)求
; (2)求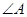 .
.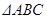 的内角
的内角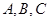 的对边分别为
的对边分别为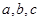 ,且
,且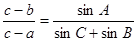 , 则
, 则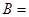 ______
______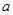 ,
,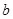 ,
,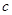 分别为
分别为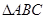 三个内角
三个内角 ,
,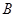 ,
,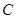 的对边,
的对边, 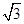
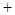
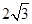 ,
,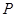 .
.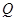 的大小; (2)求△ABC面积的最大值.
的大小; (2)求△ABC面积的最大值.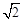 ,则
,则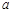 =_____________.
=_____________.