题目内容
关于函数f(x)=sin2x-(![]() )|x|+
)|x|+![]() ,有下面四个结论,其中正确结论的个数为①f(x)是奇函数 ②当x>2003时,f(x)>
,有下面四个结论,其中正确结论的个数为①f(x)是奇函数 ②当x>2003时,f(x)>![]() 恒成立 ③f(x)的最大值是
恒成立 ③f(x)的最大值是![]() ④f(x)的最小值是-
④f(x)的最小值是-![]()
[ ]
A.1
B.2
C.3
D.4
答案:A
解析:
解析:
|
显然f(x)为偶函数,结论①错.对于结论②,当x=1000π时,x>2003,sin21000π=0,∴f(1000π)= 又f(x)= ∴- 故1- 而cos2x,( 所以f(x)=1- 即结论④是正确的. |

练习册系列答案
相关题目
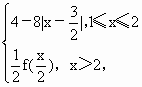 .给出下列结论:
.给出下列结论:
 x2在x=-1处取得极大值,记g(x)=
x2在x=-1处取得极大值,记g(x)= 。程序框图如图所示,若输出的结果S=
。程序框图如图所示,若输出的结果S= ,则判断框中可以填入的关于n的判断条件是( )
,则判断框中可以填入的关于n的判断条件是( )