题目内容
16.函数y=2sin(x-$\frac{π}{3}$)($\frac{π}{6}$≤x≤$\frac{2π}{3}$)的最小值是( )| A. | -2 | B. | -$\sqrt{3}$ | C. | -1 | D. | 1 |
分析 求出x-$\frac{π}{3}$的范围结合三角函数的单调性和最值的性质进行求解即可.
解答 解:∵$\frac{π}{6}$≤x≤$\frac{2π}{3}$,
∴-$\frac{π}{6}$≤x-$\frac{π}{3}$≤$\frac{π}{3}$,
∴当x-$\frac{π}{3}$=-$\frac{π}{6}$时,函数取得最小值此时y=2sin(-$\frac{π}{6}$)=-2×$\frac{1}{2}$=-1,
故选:C
点评 本题主要考查三角函数的最值的求解,求出角的范围,结合三角函数的图象和性质是解决本题的关键.

练习册系列答案
相关题目
6.如图,在三棱锥V-ABC,VA=VC,VB⊥AC,则AB与BC的大小关系是( )
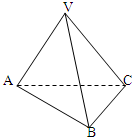

| A. | AB>BC | B. | AB=BC | C. | AB<BC | D. | 无法确定 |
4.下列命题中是真命题的是( )
| A. | 函数y=sin2x的最小正周期是2π | B. | 等差数列一定是单调数列 | ||
| C. | 直线y=ax+a过定点(-1,0) | D. | 在△ABC中,若sinB>0,则B为锐角 |
8.若loga-1(2x-1)>loga-1(x-1),则有( )
| A. | a>1,x>0 | B. | a>1,x>1 | C. | a>2,x>0 | D. | a>2,x>1 |
6.函数f(x)=3x+1的值域为( )
| A. | (-1,+∞) | B. | (1,+∞) | C. | (0,1) | D. | [1,+∞) |