题目内容
如图,在半径为 的圆
的圆 中,弦
中,弦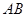 、
、 相交于
相交于 ,
, ,
, ,则圆心
,则圆心 到弦
到弦 的距离为 .
的距离为 .
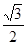
解析试题分析:由相交弦定理得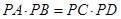 ,
,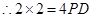 ,
,
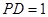 ,
,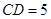 ,
, 圆心
圆心 到弦
到弦 的距离为
的距离为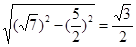 .
.
考点:圆的性质,相交弦定理.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
题目内容
如图,在半径为 的圆
的圆 中,弦
中,弦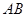 、
、 相交于
相交于 ,
, ,
, ,则圆心
,则圆心 到弦
到弦 的距离为 .
的距离为 .
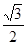
解析试题分析:由相交弦定理得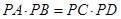 ,
,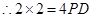 ,
,
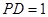 ,
,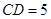 ,
, 圆心
圆心 到弦
到弦 的距离为
的距离为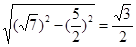 .
.
考点:圆的性质,相交弦定理.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案