题目内容
已知二次函数f（x）=ax2+bx+1和函数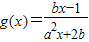
，方程g（x）=x有两个不等非零实根x1、x2（x1＜x2）．（1）证明函数f（x）在（-1，1）上是单调函数；
（2）若方程f（x）=0的两实根为x3，x4（x3＜x4），求使x3＜x1＜x2＜x4成立的a的取值范围．
【答案】分析：（1）方程g（x）=x有两个不等非零实根，说明方程a2x2+bx+1=0（*）有不等实根，由△=b2-4a2＞0，可得函数f（x）的对称轴的范围，进而根据二次函数的图象证明函数f（x）在（-1，1）上是单调函数
（2）先计算f（x1）、f（x2），再利用二次函数的图象，要使x3＜x1＜x2＜x4，只需
或
，解不等式即可
解答：解：（1）由
方程a2x2+bx+1=0（*）有不等实根∴△=b2-4a2＞0及a≠0，
，即
，或
又f（x）的对称轴
故f（x）在（-1，1）上是单调函数
（2）因x1、x2是方程（*）的根，∴a2x12+bx1+1=0∴bx1=-a2x12-1
同理bx2=-a2x22-1∴f（x1）=ax12+b1x1+1=ax12-a2x12+1=（a-a2）x12，同理f（x2）=（a-a2）x22
要使x3＜x1＜x2＜x4，只需
或
故a的取值范围a＞1
点评：本题考查了二次函数的图象和性质，解题时要熟记二次函数图象，能运用分类讨论的思想，数形结合解决问题
（2）先计算f（x1）、f（x2），再利用二次函数的图象，要使x3＜x1＜x2＜x4，只需
或，解不等式即可解答：解：（1）由
方程a2x2+bx+1=0（*）有不等实根∴△=b2-4a2＞0及a≠0，，即，或又f（x）的对称轴
故f（x）在（-1，1）上是单调函数
（2）因x1、x2是方程（*）的根，∴a2x12+bx1+1=0∴bx1=-a2x12-1
同理bx2=-a2x22-1∴f（x1）=ax12+b1x1+1=ax12-a2x12+1=（a-a2）x12，同理f（x2）=（a-a2）x22
要使x3＜x1＜x2＜x4，只需
或
故a的取值范围a＞1
点评：本题考查了二次函数的图象和性质，解题时要熟记二次函数图象，能运用分类讨论的思想，数形结合解决问题
练习册系列答案
相关题目