题目内容

【题目】已知函数,下列四个命题正确的序号是（ ）

①是偶函数 ②③当时,取得极小值④满足的正整数n的最小值为9

A.①②③B.①③④C.①②D.①②④

【答案】D

【解析】

对①,直接根据偶函数的定义判断即可.

对②,根据当时与大小关系判断即可.

对③,求导后代入判断即可.

对④,求导分析函数单调性,确定的极值点位置再判断即可.

对①, 定义域为,当时,

,故是偶函数,①正确

对②,因为为偶函数,故只需考虑时的情况即可.

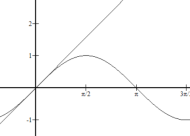
画出与的函数图像如图.因为且当时成立,由图可得当时,恒成立.

故当时,.又为偶函数,故恒成立.

对③, 令则.

当时不成立,故③错误.

对④, 令,当时,

,当时,

先画出与的图像如图

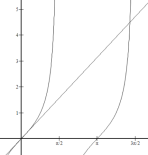
注意当时,,此时,此时

当时,,,故

当时,.故当时,

当时,,且有根.

又对,,,,,

.故满足的正整数n的最小值为9.

故④正确.

故选：D

练习册系列答案
相关题目

【题目】已知函数，.

（1）讨论的单调性；

（2）当时，记的最小值为，证明：.

【题目】已知平面向量，设函数（为常数且满足），若函数图象的一条对称轴是直线.

（1）求的值；

（2）求函数在上的最大值和最小值：

（3）证明：直线与函数的图象不相切．

【题目】已知，且，且，函数.

（1）设，，若是奇函数，求的值；

（2）设，，判断函数在上的单调性并加以证明；

（3）设，，，函数的图象是否关于某垂直于轴的直线对称？如果是，求出该对称轴，如果不是，请说明理由.

【题目】已知是公差为的等差数列，是公比为的等比数列.

（1）若，是否存在，有？请说明理由；

（2）若（、为常数，且）对任意，有，试求出、满足的充要条件；

（3）若，，试确定所有，使数列中存在某个连续项的和是数列中的一项，请证明.

【题目】若定义域均为D的三个函数f（x），g（x），h（x）满足条件：对任意x∈D，点（x，g（x）与点（x，h（x）都关于点（x，f（x）对称，则称h（x）是g（x）关于f（x）的“对称函数”．已知g（x）=，f（x）=2x+b，h（x）是g（x）关于f（x）的“对称函数”，且h（x）≥g（x）恒成立，则实数b的取值范围是_____．

【题目】在平面直角坐标系中，已知曲线上的动点到点的距离与到直线的距离相等．

（1）求曲线的轨迹方程；

（2）过点分别作射线、交曲线于不同的两点、，且．试探究直线是否过定点？如果是，请求出该定点；如果不是，请说明理由．

【题目】已知．

（1）若在上恒成立，求实数的取值范围；

（2）证明：当时，．

【题目】下列叙述正确的是（ ）

A.命题“p且q”为真，则恰有一个为真命题

B.命题“已知，则“”是“”的充分不必要条件”

C.命题都有，则，使得

D.如果函数在区间上是连续不断的一条曲线，并且有，那么函数在区间内有零点

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网