题目内容
已知向量 ,
, .
.
(1)若 ,求
,求 的值;
的值;
(2)若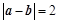 ,
, ,求
,求 的值.
的值.
(1) ;(2)
;(2)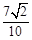 .
.
解析试题分析:(1)由 易得
易得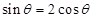 ,代入式子
,代入式子 中可约去为
中可约去为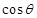 求出其值;(2)先求出
求出其值;(2)先求出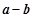 ,再对
,再对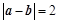 两边平方化简可得关于
两边平方化简可得关于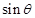 和
和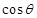 的关系式,联立正弦余弦的平方关系解方程组可得
的关系式,联立正弦余弦的平方关系解方程组可得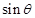 和
和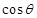 的值,代入
的值,代入 的展开式,就可求出其值.
的展开式,就可求出其值.
试题解析:⑴由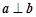 可知,
可知,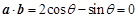 ,所以
,所以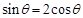 , 2分
, 2分
所以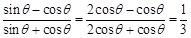 . 6分
. 6分
(2)由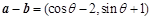 可得,
可得,
 ,
,
即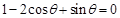 , ① 10分
, ① 10分
又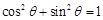 ,且
,且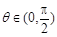 ②,由①②可解得,
②,由①②可解得,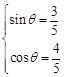 , 12分
, 12分
所以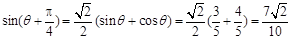 . 14分
. 14分
考点:向量的数量积、模的计算,同角三角函数的关系、两角和与差的正弦.

练习册系列答案
相关题目

 的最小正周期;
的最小正周期; ,求
,求 的值域.
的值域. ;
; ;
; ;
; ;
; .
.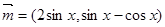 ,
, ,函数
,函数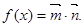
 的解析式;
的解析式; 中,角
中,角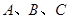 的对边为
的对边为 ,若
,若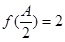 ,
,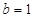 ,
,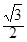 ,求a的值.
,求a的值. 中,
中, 分别为角
分别为角 的对边,且
的对边,且 .
. 的最大值.
的最大值.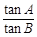 =
=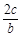 .
.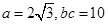 ,求
,求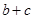 的值。
的值。
 时,求函数
时,求函数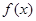 的值域;
的值域; 的图象向左平移
的图象向左平移 个单位得到函数
个单位得到函数 的图象,再将
的图象,再将 的图象,求证:直线
的图象,求证:直线 与
与
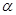 为第二象限的角,
为第二象限的角,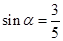 ,
,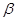 为第一象限的角,
为第一象限的角,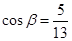 .求
.求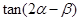
 的值.
的值. sin2
sin2 +cos
+cos