题目内容
已知:等差数列{an}中,a3+a4=15,a2a5=54,公差d<0.
(I)求数列{an}的通项公式an;
(II)求数列的前n项和Sn的最大值及相应的n的值.
(1) ;(2)
;(2) 或11时,
或11时, 取得最大值,最大值为55.
取得最大值,最大值为55.
解析试题分析:(1)根据等差数列的通项公式由a3+a4=15,a2a5=54得一方程组,解这个方程组得公差和首项,从而得数列{an}的通项公式an.
(2)等差数列的前n项和Sn是关于n的二次式,将这个二次式配方即可得最大值.
试题解析:(1)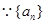 为等差数列,
为等差数列,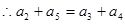
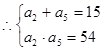 解得
解得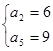 (因d<0,舍去)
(因d<0,舍去)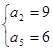

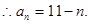 6分
6分
(2)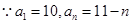 ,
,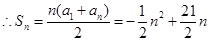 9分
9分
又 ,对称轴为
,对称轴为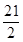 ,故当
,故当 或11时,
或11时,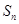 取得最大值,最大值为55 12分
取得最大值,最大值为55 12分
考点:等差数列

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
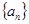 中满足
中满足 ,
,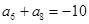 .
.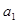 和公差
和公差 ;
; 0的等差数列,且它的第2、3、6项依次构成等比数列{bn}的前3项。
0的等差数列,且它的第2、3、6项依次构成等比数列{bn}的前3项。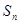 是各项均为非零实数的数列
是各项均为非零实数的数列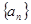 的前
的前 项和,给出如下两个命题上:
项和,给出如下两个命题上: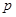 :
: :等式
:等式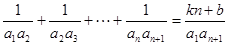 对任意
对任意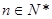 )恒成立,其中
)恒成立,其中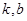 是常数。
是常数。 与
与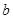 ,问
,问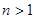 )和正数M,数列
)和正数M,数列 ,试求
,试求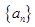 中,已知
中,已知 ,
,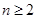 时,
时,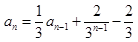 .数列
.数列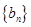 满足:
满足: .
.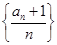 的前
的前 项和为
项和为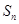 ,若不等式
,若不等式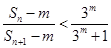 成立(
成立(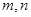 为正整数).求出所有符合条件的有序实数对
为正整数).求出所有符合条件的有序实数对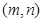 .
. 中,公差
中,公差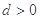 ,其前
,其前 项和为
项和为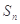 ,且满足:
,且满足: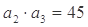 ,
, .
. ,
, ,求
,求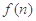 的最小值.
的最小值. 满足
满足 ,且对任意非负整数
,且对任意非负整数 均有:
均有: .
. ;
; 是等差数列,并求
是等差数列,并求 的通项;
的通项; ,求证:
,求证: .
. 的前
的前 项和为
项和为 ,且
,且 ,数列
,数列 满足
满足 ,且点
,且点 在直线
在直线 上.
上. 的前
的前 .
. ,公差
,公差 不为零,
不为零,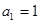 ,且
,且 成等比数列;
成等比数列; 满足
满足 ,求数列
,求数列 项和
项和 .
.