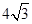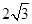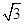题目内容
在△ABC中,∠C=90°,M是BC的中点.若sin∠BAM=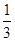 ,则sin∠BAC=________.
,则sin∠BAC=________.
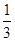 ,则sin∠BAC=________.
,则sin∠BAC=________.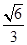
因为sin∠BAM=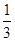 ,所以cos∠BAM=
,所以cos∠BAM=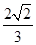 .在△ABM中,利用正弦定理,得
.在△ABM中,利用正弦定理,得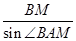 =
=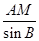 ,所以
,所以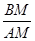 =
=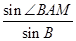 =
=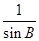 =
=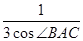 .
.
在Rt△ACM中,有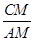 =sin∠CAM=sin(∠BAC-∠BAM).由题意知BM=CM,所以
=sin∠CAM=sin(∠BAC-∠BAM).由题意知BM=CM,所以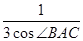 =sin(∠BAC-∠BAM).
=sin(∠BAC-∠BAM).
化简,得2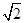 sin∠BACcos∠BAC-cos2∠BAC=1.
sin∠BACcos∠BAC-cos2∠BAC=1.
所以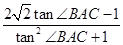 =1,解得tan∠BAC=
=1,解得tan∠BAC=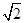 .
.
再结合sin2∠BAC+cos2∠BAC=1,∠BAC为锐角可解得sin∠BAC=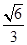 .
.
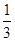 ,所以cos∠BAM=
,所以cos∠BAM=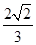 .在△ABM中,利用正弦定理,得
.在△ABM中,利用正弦定理,得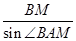 =
=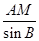 ,所以
,所以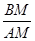 =
=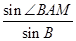 =
=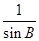 =
=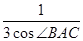 .
.在Rt△ACM中,有
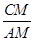 =sin∠CAM=sin(∠BAC-∠BAM).由题意知BM=CM,所以
=sin∠CAM=sin(∠BAC-∠BAM).由题意知BM=CM,所以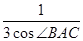 =sin(∠BAC-∠BAM).
=sin(∠BAC-∠BAM).化简,得2
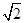 sin∠BACcos∠BAC-cos2∠BAC=1.
sin∠BACcos∠BAC-cos2∠BAC=1.所以
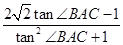 =1,解得tan∠BAC=
=1,解得tan∠BAC=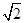 .
.再结合sin2∠BAC+cos2∠BAC=1,∠BAC为锐角可解得sin∠BAC=
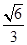 .
.
练习册系列答案
相关题目
 中,
中,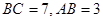 ,且
,且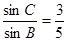 .
.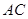 ; (2)求
; (2)求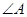 .
. 中,若
中,若 ,
, ,则
,则 的值为( )
的值为( )



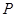 .
.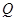 的大小; (2)求△ABC面积的最大值.
的大小; (2)求△ABC面积的最大值. 中,角
中,角 ,
, ,
,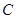 的对边分别是
的对边分别是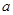 ,
,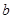 ,
,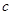 ,且
,且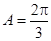 ,
,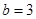 ,△
,△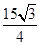 .
.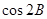 的值.
的值.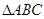 中,边
中,边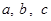 所对角分别为
所对角分别为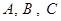 ,若
,若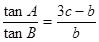 ,
,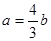 ,则
,则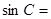 ( )
( )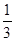
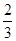
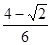
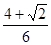
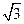 a+c,sinB-sinA),若m∥n,则角B的大小为( )
a+c,sinB-sinA),若m∥n,则角B的大小为( )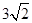 ,则AC=
,则AC=