题目内容
已知a<b函数 ,若命题
,若命题 ,命题q:g(x)在 (a,b) 内有最值,则命题p是命题q成立的( )
,命题q:g(x)在 (a,b) 内有最值,则命题p是命题q成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:∵f(a)•f(b)<0,
又∵f(x)在R上连续
根据函数的零点判定定理可知,函数f(x)在(a,b)上存在零点
根据正弦函数、余弦函数的性质可知,正弦函数的零点是余弦函数的最值点
∴g(x)=cosx在(a,b)上有最值,∴p⇒q
若g(x)=cosx在(a,b)上有最值则根据余弦函数的零点是正弦函数的零点
则f(x)=sinx在(a,b)上有零点,但是由于函数f(x)=sinx在(a,b)不一定单调,f(a)f(b)<0不一定成立
故命题p:f(a)•f(b)<0,命题q:函数g(x)在区间(a,b)内有最值的充分不必要条件,故选A
考点:本试题主要考查了充分条件与必要条件的判断.
点评:解题的关键是准确、熟练的应用函数的零点定理及正弦函数与余弦函数的性质分析和解决问题。由f(a)•f(b)<0,及f(x)在R上连续可知函数f(x)在(a,b)上存在零点,然后结合正弦函数的零点是余弦函数的最值点可判断,若g(x)=cosx在(a,b)上有最值,f(x)=sinx在(a,b)上有零点,但由于函数f(x)=sinx在(a,b)不一定单调,f(a)f(b)<0不一定成立

下列有关命题的说法中错误的是( )
| A.“若x2+y2=0,则x,y全为0”的否命题是真命题 |
B.“ ”是“ ”是“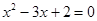 ”的必要不充分条件 ”的必要不充分条件 |
C.命题“若 ,则 ,则 “的逆否命题为:“若 “的逆否命题为:“若 则 则 ” ” |
D.对于命题 使得 使得 ,则 ,则 均有 均有 |
命题 的否定是( )
的否定是( )
A. | B. |
C. | D.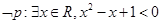 |
“m=4”是“直线(m+2)x+2my-1=0与直线(m+ )x+(m+2)y+3=0相互平行”的
)x+(m+2)y+3=0相互平行”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要 |
设p: , q:
, q: ,则p是q的
,则p是q的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
在 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“ ”是“
”是“ ”的( )
”的( )
| A.充要条件 | B.必要而不充分条件 |
| C.充分而不必要条件 | D.既不充分也不必要 |
下列命题中,正确的命题有 ( )
①用相关系数 来判断两个变量的相关性时,
来判断两个变量的相关性时, 越接近0,说明两个变量有较强的相关性;
越接近0,说明两个变量有较强的相关性;
②将一组数据中的每个数据都加上同一个常数后,方差恒不变;
③设随机变量 服从正态分布N(0,1),若
服从正态分布N(0,1),若 ;
;
④回归直线一定过样本点的中心
| A.1个 | B.2个 | C.3个 | D.4个 |
设 是平面
是平面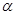 内两条不同的直线,
内两条不同的直线, 是平面
是平面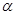 外的一条直线,则“
外的一条直线,则“ ,
, ”是“
”是“ ”的( )
”的( )
| A.充要条件 | B.充分而不必要的条件 |
| C.必要而不充分的条件 | D.既不充分也不必要的条件 |