题目内容
命题
的否定是（ ）
A． | B． |
C． | D． |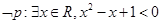
B
解析试题分析：因为命题的否定是特称命题，因此将任意改为存在，结论变为否定即可。故可知其否定为，故选B.
考点：本题主要考查命题的否定，是一个基础题.
点评：解决该试题的关键是根据所给的这个命题是全称命题，它的否定形式是特称命题，改为特称命题，注意题设和结论的变化．
练习册系列答案
相关题目
在空间，下列命题正确的是 （ ）
| A．平行直线的平行投影重合； | B．平行于同一直线的两个平面平行； |
| C．垂直于同一平面的两个平面平行； | D．垂直于同一平面的两条直线平行． |
下列命题中,真命题是
A． | B． |
C． 的充要条件是 | D． 是 的充分条件 |
给定下列命题：①全等的两个三角形面积相等；②3的倍数一定能被6整除；③如果
，那么
；④若
，则
。其中，真命题有
| A．① | B．①③④ | C．①④ | D．①②③④ |
在下列结论中，正确的结论为（ ）
（1）“
”为真是“
”为真的充分不必要条件
（2）“”为假是“”为真的充分不必要条件
（3）“”为真是“
”为假的必要不充分条件
（4）“”为真是“”为假的必要不充分条件
| A．（1）（2） | B．（1）（3） | C．（2）（4） | D．（3）（4） |
命题“存在
,使
”的否定是（ ）
A．存在,使 | B．不存在,使 |
| C．对于任意 ,都有 | D．对于任意,都有 |
如果命题“非p”与命题“p或q”都是真命题，那么（ ）
| A．命题p与命题q的真值相同 | B．命题q一定是真命题 |
| C．命题q不一定是真命题 | D．命题p不一定是真命题 |
已知a<b函数
，若命题
，命题q:g(x)在 (a，b) 内有最值，则命题p是命题q成立的( )
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
在命题“方程x
=4的解是x=±2”中，逻辑联结词的使用情况是（ ）
| A．使用了逻辑联结词“或” | B．使用了逻辑联结词“且” |
| C．使用了逻辑联结词“非” | D．未使用逻辑联结词“或”、“且”、“非” |