题目内容
若M为椭圆上一点，F1，F2是椭圆的两个焦点，且∠MF1F2=2∠MF2F1=2α（α≠0），则椭圆的离心离是________．
2cosα-1
分析：应用正弦定理找出MF1和 MF2的关系，利用椭圆定义及焦距的长，得到2个等式，把这2个等式相除便可得到离心率的表达式，化简可求离心率．
解答：设MF1=m，MF2=n，由正弦定理得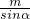
=
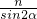，∴n=2mcosα．
又由椭圆的定义知，m+2mcosα=2a，再由 mcos2α+2mcosα•cosα=2c 可得，
∴e=
=
=
=
=
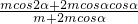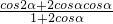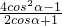=2cosα-1，
故答案为 2cosα-1．
点评：本题主要考查椭圆的定义和性质，及三角形中的正弦定理的应用，属于中档题．
分析：应用正弦定理找出MF1和 MF2的关系，利用椭圆定义及焦距的长，得到2个等式，把这2个等式相除便可得到离心率的表达式，化简可求离心率．
解答：设MF1=m，MF2=n，由正弦定理得
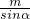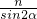=，∴n=2mcosα．又由椭圆的定义知，m+2mcosα=2a，再由 mcos2α+2mcosα•cosα=2c 可得，
∴e=
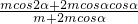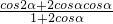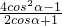=====2cosα-1，故答案为 2cosα-1．
点评：本题主要考查椭圆的定义和性质，及三角形中的正弦定理的应用，属于中档题．
练习册系列答案
相关题目
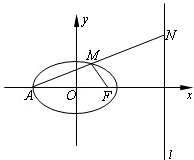如图，已知椭圆
如图，已知椭圆C：
上一点，F为右焦点，若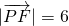
，且点M满足
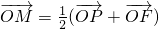（其中O为坐标原点），则
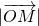的值为