题目内容
下列说法错误的是( )
分析:A:由特殊角的三角函数得:“sinθ=
”是“θ=30°”的必要不充分条件.
B:根据否命题的概念可得对原命题的条件与结论都进行否定,即可得到原命题的否命题.
C:特称命题的否定是全称命题.
D:如果命题“?p”是真命题,则p是假命题,又因为命题“p或q”是真命题,所以q是真命题.
| 1 |
| 2 |
B:根据否命题的概念可得对原命题的条件与结论都进行否定,即可得到原命题的否命题.
C:特称命题的否定是全称命题.
D:如果命题“?p”是真命题,则p是假命题,又因为命题“p或q”是真命题,所以q是真命题.
解答:解:A:由特殊角的三角函数得:若sinθ=
,则θ不一定为30°;但是若θ=30°,则sinθ=
,所以“sinθ=
”是“θ=30°”的必要不充分条件,所以选A.
B:根据否命题的概念可得对原命题的条件与结论都进行否定,即可得到原命题的否命题,所以不选B.
C:根据特称命题的否定是全称命题可得:若命题p:?x∈R,x2-x+1<0,则?p:?x∈R,x2-x+1≥0是正确的,所以C不能选.
D:如果命题“?p”是真命题,则p是假命题,又因为命题“p或q”是真命题,所以q是真命题,所以不选D.
故选A.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
B:根据否命题的概念可得对原命题的条件与结论都进行否定,即可得到原命题的否命题,所以不选B.
C:根据特称命题的否定是全称命题可得:若命题p:?x∈R,x2-x+1<0,则?p:?x∈R,x2-x+1≥0是正确的,所以C不能选.
D:如果命题“?p”是真命题,则p是假命题,又因为命题“p或q”是真命题,所以q是真命题,所以不选D.
故选A.
点评:本题主要考查必要条件、充分条件、充要条件的判断与复合命题的真假,以及四种命题、特称命题的否命题,此题属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
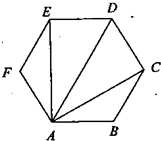 在正六边形ABCDEF中(如图),下列说法错误的是( )
在正六边形ABCDEF中(如图),下列说法错误的是( )