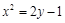题目内容
设 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 为直线
为直线 上一点,
上一点,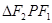 是底角为
是底角为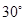 的等腰三角形,则
的等腰三角形,则 的离心率为 ( )
的离心率为 ( )
A. | B. | C. | D. |
C
解析试题分析:利用椭圆的离心率定义并结合图形求解
如右图,知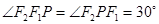 ,所以
,所以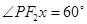
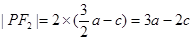
因为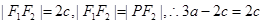
所以
考点:本小题主要考查了椭圆几何性质、离心率的概念及求法,同时考查了数形结合思想。
点评:解决此类问题的关键是掌握离心率的概念。努力寻找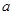 与
与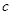 的关系,构造出关于
的关系,构造出关于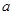 与
与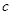 的方程,同时对数形结合思想要有较深刻的理解与应用能力,难度一般。
的方程,同时对数形结合思想要有较深刻的理解与应用能力,难度一般。

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
若点 和点
和点 分别为双曲线
分别为双曲线 (
( )的中心和左焦点,点
)的中心和左焦点,点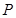 为双曲线右支上的任意一点,则
为双曲线右支上的任意一点,则 的取值范围为( )
的取值范围为( )
A.[3-  , ,  ) ) | B.[3+  , ,  ) ) |
C.[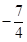 , ,  ) ) | D.[ , ,  ) ) |
抛物线 (p>0)上一点M到焦点的距离是a,则M到y轴的距离是( )
(p>0)上一点M到焦点的距离是a,则M到y轴的距离是( )
| A.a-p | B. a+p | C.a-  | D.a+2p |
若点 和点
和点 分别为椭圆
分别为椭圆 的中心和左焦点,点
的中心和左焦点,点 为椭圆上的任意一点, 则
为椭圆上的任意一点, 则 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
已知P是以F1、F2为焦点的双曲线 上一点,若
上一点,若 ,则三角形
,则三角形 的面积为( )
的面积为( )
| A.16 | B. | C. | D. |
抛物线 的焦点坐标为( )
的焦点坐标为( )
A. | B. | C.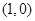 | D. |
设 、
、 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 为直线
为直线 上一点,
上一点, 是底角为
是底角为 的等腰三角形,则
的等腰三角形,则 的离心率为( )
的离心率为( )
A. | B. | C.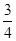 | D. |
 上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是( )
上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是( )
 是抛物线
是抛物线 的焦点,
的焦点, 是该抛物线上的动点,则线段
是该抛物线上的动点,则线段 中点的轨迹方程是( )
中点的轨迹方程是( )