题目内容
已知P是以F1、F2为焦点的双曲线 上一点,若
上一点,若 ,则三角形
,则三角形 的面积为( )
的面积为( )
| A.16 | B. | C. | D. |
B
解析试题分析:由双曲线的定义可知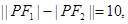 ….(1)
….(1)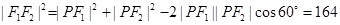 (2)
(2)
所以(1)平方减去(2)式可得 .
.
考点:双曲线的定义,余弦定理,三角形的面积公式.
点评:根据双曲线的定义及余弦定理可推导出焦点三角形的面积公式: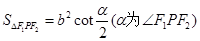 .
.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
抛物线 的焦点坐标是( )
的焦点坐标是( )
A. | B. | C. | D. |
抛物线 截直线
截直线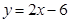 所得的弦长等于
所得的弦长等于
A. | B. | C. | D.15 |
抛物线 的焦点到准线的距离是 ( )
的焦点到准线的距离是 ( )
A.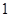 | B. | C.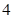 | D. |
设 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 为直线
为直线 上一点,
上一点,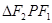 是底角为
是底角为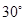 的等腰三角形,则
的等腰三角形,则 的离心率为 ( )
的离心率为 ( )
A. | B. | C. | D. |
过点 且与双曲线
且与双曲线 -y
-y =1有公共渐近线的双曲线方程是( )
=1有公共渐近线的双曲线方程是( )
A. - -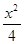 =1 =1 | B. - - =1 =1 |
C.y - - =1 =1 | D. - -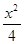 =1或 =1或 - - =1 =1 |
已知点 在椭圆
在椭圆 上,则
上,则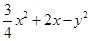 的最大值为( )
的最大值为( )
A. | B.-1 | C.2 | D.7 |
抛物线 的焦点到准线的距离为( )
的焦点到准线的距离为( )
| A.1 | B. | C. | D.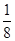 |
设椭圆 的右焦点与抛物线
的右焦点与抛物线 的焦点相同,离心率为
的焦点相同,离心率为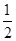 ,则此椭圆的方程为( )
,则此椭圆的方程为( )
A. | B. | C.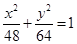 | D. |