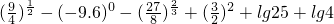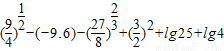题目内容
求式子(|x|+| 1 | |x| |
分析:解法一:利用分步乘法原理展开式中的常数项是三种情况的和,
解法二:先将(|x|+
-2)2利用完全平方公式化成二项式,利用二项展开式的通项公式求得第r+1项,令x的指数为0得常数项.
解法二:先将(|x|+
| 1 |
| |x| |
解答:解法一:(|x|+
-2)3=(|x|+
-2)(|x|+
-2)(|x|+
-2)得到常数项的情况有:
①三个括号中全取-2,得(-2)3;
②一个括号取|x|,一个括号取
,一个括号取-2,得C31C21(-2)=-12,
∴常数项为(-2)3+(-12)=-20.
解法二:(|x|+
-2)3=(
-
)6.
设第r+1项为常数项,
则Tr+1=C6r•(-1)r•(
)r•|x|6-r=(-1)6•C6r•|x|6-2r,得6-2r=0,r=3.
∴T3+1=(-1)3•C63=-20.
| 1 |
| |x| |
| 1 |
| |x| |
| 1 |
| |x| |
| 1 |
| |x| |
①三个括号中全取-2,得(-2)3;
②一个括号取|x|,一个括号取
| 1 |
| |x| |
∴常数项为(-2)3+(-12)=-20.
解法二:(|x|+
| 1 |
| |x| |
| |x| |
| 1 | ||
|
设第r+1项为常数项,
则Tr+1=C6r•(-1)r•(
| 1 |
| |x| |
∴T3+1=(-1)3•C63=-20.
点评:本题考查解决二项展开式的特定项问题的重要工具有二项展开式的通项公式;还有分步乘法原理.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目