题目内容
求下列各式的值.(1)
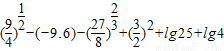
(2)已知x+x-1=3,求式子x2+x-2的值.
【答案】分析:(1)直接利用有理指数幂的运算性质和对数的运算性质化简求值.
(2)把已知的等式两边平方即可求得x2+x-2的值.
解答:解:(1)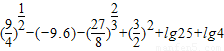
=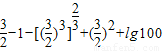
=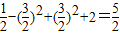 ;
;
(2)由x+x-1=3,两边平方得x2+2+x-2=9,
所以x2+x-2=7.
点评:本题考查了有理指数幂的化简求值,考查了对数的运算性质,是基础的计算题.
(2)把已知的等式两边平方即可求得x2+x-2的值.
解答:解:(1)
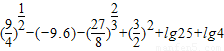
=
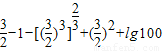
=
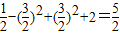 ;
;(2)由x+x-1=3,两边平方得x2+2+x-2=9,
所以x2+x-2=7.
点评:本题考查了有理指数幂的化简求值,考查了对数的运算性质,是基础的计算题.

练习册系列答案
相关题目