题目内容
当不等式组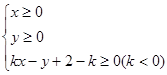
所表示的平面区域的面积最小时,实数k的值为( )
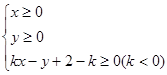所表示的平面区域的面积最小时,实数k的值为( ) A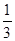．－ | B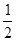．－ | C．－1 | D．－2 |
D
由于不等式组所表示的平面区域由三条直线围成，其中直线kx-y+2-k=0（k＜0）即y-2=k（x-1）（k＜0）经过定点（1，2），
因此问题转化为求经过定点（1，2）的直线与两坐标轴在第一象限内所围成的三角形的面积的最小值．
如图所示，设所围成的区域的面积为S，则S=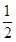
•|OA|•|OB|=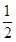•|2-k|•|1-
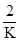|．因为k＜0，所以-k＞0，当S取得最小值4时，-k=-
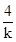，解得k=-2． 选D
因此问题转化为求经过定点（1，2）的直线与两坐标轴在第一象限内所围成的三角形的面积的最小值．
如图所示，设所围成的区域的面积为S，则S=
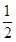•|OA|•|OB|=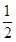•|2-k|•|1-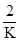|．因为k＜0，所以-k＞0，当S取得最小值4时，-k=-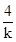，解得k=-2． 选D
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
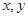满足线性约束条件
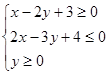,若目标函数
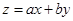(其中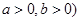
的最大值为3,则
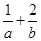的最小值为
。
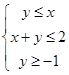下,过点
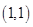目标函数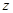
取得最大值10,则目标函数
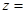______（写出一个适合题意的目标函数即可）；
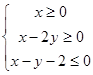，则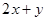
的最小值为__________ -
，
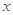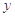满足约束条件
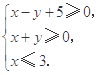求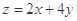
的最小值与最大值。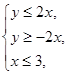
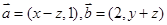，且
，若变量x,y满足约束条件
则z的最大值为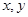
满足
则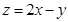
的取值范围是____________.