题目内容
若函数 在
在 上单调递增,那么实数
上单调递增,那么实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
A
解析试题分析: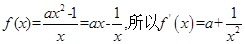 ,因为函数
,因为函数 在
在 上单调递增,所以
上单调递增,所以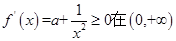 恒成立且不恒为零,即
恒成立且不恒为零,即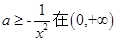 内恒成立且不恒为零,所以
内恒成立且不恒为零,所以 ,
,
考点:利用导数研究函数的单调性。
点评:注意:由“函数 在
在 上单调递增”应该得到的是:“
上单调递增”应该得到的是:“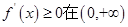 内恒成立且不恒为零”。不少同学这个地方出错,错误的认为应得到
内恒成立且不恒为零”。不少同学这个地方出错,错误的认为应得到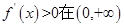 内恒成立。
内恒成立。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数 ,则函数
,则函数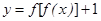 的零点个数是( )
的零点个数是( )
| A.4 | B.3 | C.2 | D.1 |
已知 ,
, ,
, ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |
若函数 的两个零点是2和3,则函数
的两个零点是2和3,则函数 的零点是( )
的零点是( )
A.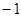 和 和 | B. 和 和 | C. 和 和 | D. 和 和 |
已知点 ,
, ,若点
,若点 在函数
在函数 的图象上,则使得
的图象上,则使得 的面积为2的点
的面积为2的点 的个数为
的个数为
| A.4 | B.3 | C.2 | D.1 |
若 ,则
,则 属于区间( )
属于区间( )
A.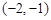 | B. | C. | D. |
数 的单调递增区间为( )
的单调递增区间为( )
| A.(-∞,1) | B.(2,+∞) | C.(-∞, ) ) | D.( ,+∞) ,+∞) |
设 ,则( )
,则( )
A. | B. |
C. | D. |
 的图象大致是( )
的图象大致是( )


