题目内容
)设点C为曲线y=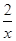 (x>0)上任一点,以点C为圆心的圆与x轴交于点E、A,与y轴交于点E、B.
(x>0)上任一点,以点C为圆心的圆与x轴交于点E、A,与y轴交于点E、B.
(1)证明:多边形EACB的面积是定值,并求这个定值;
(2)设直线y=-2x+4与圆C交于点M,N,若|EM|=|EN|,求圆C的方程.
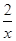 (x>0)上任一点,以点C为圆心的圆与x轴交于点E、A,与y轴交于点E、B.
(x>0)上任一点,以点C为圆心的圆与x轴交于点E、A,与y轴交于点E、B.(1)证明:多边形EACB的面积是定值,并求这个定值;
(2)设直线y=-2x+4与圆C交于点M,N,若|EM|=|EN|,求圆C的方程.
(1)见解析;(2)(x-2)2+(y-1)2=5.
(1)可直接确定点E为原点,所以设圆心C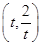 ,然后根据半径长度为|OC|,即可写出圆的标准方程 ,然后再求四边形的面积看是否是定值即可。
,然后根据半径长度为|OC|,即可写出圆的标准方程 ,然后再求四边形的面积看是否是定值即可。
(2)根据圆的几何性质可知CE所在直线与直线y=-2x+4垂直,所以根据斜率积为-1,即可求出t的值,进而确定圆的方程。
解:(1)证明:设点C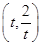 (t>0),因为以点C为圆心的圆与x轴交于点E、A,与y轴交于点E、B.
(t>0),因为以点C为圆心的圆与x轴交于点E、A,与y轴交于点E、B.
所以,点E是直角坐标系原点,即E(0,0).
于是圆C的方程是(x-t)2+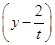 2=t2+
2=t2+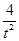 .
.
则A(2t,0),B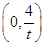 .
.
由|CE|=|CA|=|CB|知,圆心C在Rt△AEB的斜边AB上,于是多边形EACB为Rt△AEB,
其面积S=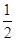 |EA|·|EB|=
|EA|·|EB|=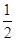 ×2t×
×2t×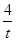 =4.
=4.
所以多边形EACB的面积是定值,这个定值是4.
(2)若|EM|=|EN|,则E在MN的垂直平分线上,即EC是MN的垂直平分线.
因为kEC=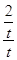 =
=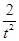 ,kMN=-2.
,kMN=-2.
所以由kEC·kMN=-1得t=2.
所以圆C的方程是(x-2)2+(y-1)2=5.
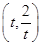 ,然后根据半径长度为|OC|,即可写出圆的标准方程 ,然后再求四边形的面积看是否是定值即可。
,然后根据半径长度为|OC|,即可写出圆的标准方程 ,然后再求四边形的面积看是否是定值即可。(2)根据圆的几何性质可知CE所在直线与直线y=-2x+4垂直,所以根据斜率积为-1,即可求出t的值,进而确定圆的方程。
解:(1)证明:设点C
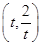 (t>0),因为以点C为圆心的圆与x轴交于点E、A,与y轴交于点E、B.
(t>0),因为以点C为圆心的圆与x轴交于点E、A,与y轴交于点E、B.所以,点E是直角坐标系原点,即E(0,0).
于是圆C的方程是(x-t)2+
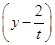 2=t2+
2=t2+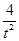 .
.则A(2t,0),B
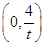 .
.由|CE|=|CA|=|CB|知,圆心C在Rt△AEB的斜边AB上,于是多边形EACB为Rt△AEB,
其面积S=
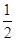 |EA|·|EB|=
|EA|·|EB|=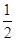 ×2t×
×2t×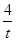 =4.
=4.所以多边形EACB的面积是定值,这个定值是4.
(2)若|EM|=|EN|,则E在MN的垂直平分线上,即EC是MN的垂直平分线.
因为kEC=
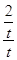 =
=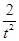 ,kMN=-2.
,kMN=-2.所以由kEC·kMN=-1得t=2.
所以圆C的方程是(x-2)2+(y-1)2=5.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 (
( 为参数)的倾斜角的大小.
为参数)的倾斜角的大小.  ,
, 是曲线
是曲线 上任意一点,求
上任意一点,求 的面积的最小值.
的面积的最小值.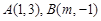 ,直线
,直线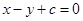 将这两圆的面积均平分,则
将这两圆的面积均平分,则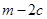 的值是( )
的值是( )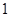
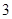
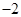
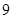
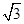 y+1+m=0与圆x2+y2=m的位置关系是( )
y+1+m=0与圆x2+y2=m的位置关系是( ) 的形状;
的形状;
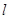 :x-y+2=0的对称点都在圆C上,则a= .
:x-y+2=0的对称点都在圆C上,则a= . 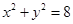 内有一点P(-1,2),弦AB为过点P.
内有一点P(-1,2),弦AB为过点P.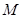 ,求点
,求点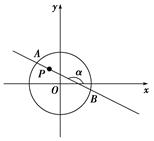
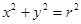 与直线
与直线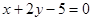 相交于
相交于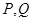 两点, 若
两点, 若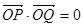 (
(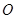 为原点),则圆的半径
为原点),则圆的半径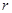 值的为 ;
值的为 ; 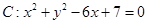 的切线,切点分别为A和B,点Q是圆C上一点,则
的切线,切点分别为A和B,点Q是圆C上一点,则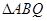 面积的最大值为 。
面积的最大值为 。