题目内容
设两个非零向量a与b不共线.
(1)若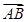 =a+b,
=a+b,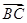 =2a+8b,
=2a+8b,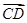 =3(a-b).求证:A、B、D三点共线;
=3(a-b).求证:A、B、D三点共线;
(2)试确定实数k,使ka+b和a+kb共线.
(1)若
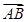 =a+b,
=a+b,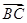 =2a+8b,
=2a+8b,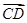 =3(a-b).求证:A、B、D三点共线;
=3(a-b).求证:A、B、D三点共线;(2)试确定实数k,使ka+b和a+kb共线.
(1)见解析(2)k=±1
(1)证明:∵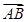 =a+b,
=a+b,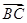 =2a+8b,
=2a+8b,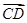 =3(a-b),
=3(a-b),
∴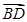 =
=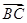 +
+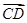 =2a+8b+3(a-b)=5(a+b)=5
=2a+8b+3(a-b)=5(a+b)=5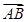 .
.
∴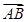 ,
,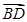 共线.
共线.
又它们有公共点B,∴A、B、D三点共线.
(2)解:∵ka+b与a+kb共线,
∴存在实数λ,使ka+b=λ(a+kb),
即(k-λ)a=(λk-1)b.
又a、b是两不共线的非零向量,
∴k-λ=λk-1=0.
∴k2-1=0.∴k=±1.
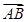 =a+b,
=a+b,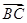 =2a+8b,
=2a+8b,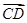 =3(a-b),
=3(a-b),∴
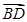 =
=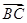 +
+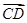 =2a+8b+3(a-b)=5(a+b)=5
=2a+8b+3(a-b)=5(a+b)=5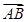 .
.∴
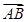 ,
,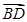 共线.
共线.又它们有公共点B,∴A、B、D三点共线.
(2)解:∵ka+b与a+kb共线,
∴存在实数λ,使ka+b=λ(a+kb),
即(k-λ)a=(λk-1)b.
又a、b是两不共线的非零向量,
∴k-λ=λk-1=0.
∴k2-1=0.∴k=±1.

练习册系列答案
相关题目
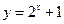 的图象按向量
的图象按向量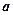 平移得到函数
平移得到函数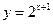 的
的 .
. 的是( )
的是( )



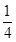
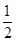
 中,
中,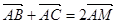 ,
, 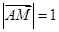 ,点
,点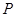 在
在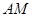 上且满足
上且满足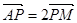 ,则
,则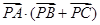 等于( )
等于( )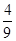
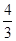

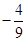
 外接圆的半径为1,圆心为O.且
外接圆的半径为1,圆心为O.且 ,则
,则 等于( )
等于( )


 的外接圆的圆心为
的外接圆的圆心为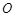 ,半径为
,半径为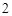 ,
,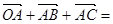 0且
0且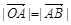 ,则向量
,则向量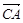 在
在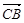 方向上的投影为______.
方向上的投影为______. 中,
中,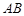 ∥
∥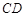 ,
,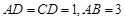 ,动点
,动点 在
在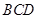 内运动(含边界),设
内运动(含边界),设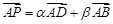 ,则
,则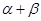 的最大值是 .
的最大值是 .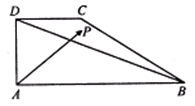
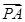 +3
+3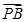 +4
+4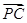 =3
=3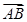 ,则△PAB与△PBC的面积的比值为__________.
,则△PAB与△PBC的面积的比值为__________.