题目内容
已知函数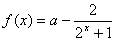 ,
,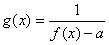 。
。
(1)若函数f(x)为奇函数,求a的值;
(2)若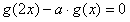 ,有唯一实数解,求a的取值范围;
,有唯一实数解,求a的取值范围;
(3)若a=2,则是否存在实数m,n(m<n<0),使得函数y=f(x)的定义域和值域都为[m,n]。若存在,求出m,n的值;若不存在,请说明理由。
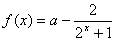 ,
,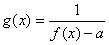 。
。(1)若函数f(x)为奇函数,求a的值;
(2)若
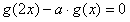 ,有唯一实数解,求a的取值范围;
,有唯一实数解,求a的取值范围;(3)若a=2,则是否存在实数m,n(m<n<0),使得函数y=f(x)的定义域和值域都为[m,n]。若存在,求出m,n的值;若不存在,请说明理由。
解:(1)∵f(x)为奇函数,
∴f(-x)=-f(x),
∴f(0)=0,
∴a=1。
(2) ,
,
∴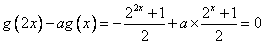 ,
,
令 ,
,
则问题转化为方程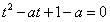 在
在 上有唯一解,
上有唯一解,
令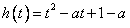 ,则
,则 ,
,
∴a≥1。
(3)不存在实数m、n满足题意。
易知 ,
,
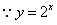 在R上是增函数,
在R上是增函数,
∴f(x)在R上是增函数,
假设存在实数m、n(m<n<0)满足题意,有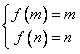 ,
,
即m、n是方程f(x)=x的两个不等负根。
由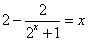 ,得
,得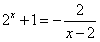 ,
,
令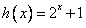 ,
,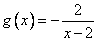 ,
,
因为函数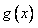 在
在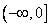 上为单调递增函数,
上为单调递增函数,
∴当x<0时,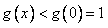 ,
,
而 ,∴
,∴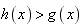 ,
,
∴方程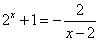 在
在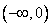 上无解,故不存在实数m、n满足题意。
上无解,故不存在实数m、n满足题意。
∴f(-x)=-f(x),
∴f(0)=0,
∴a=1。
(2)
 ,
,∴
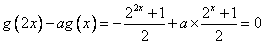 ,
,令
 ,
,则问题转化为方程
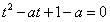 在
在 上有唯一解,
上有唯一解,令
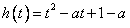 ,则
,则 ,
,∴a≥1。
(3)不存在实数m、n满足题意。
易知
 ,
,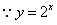 在R上是增函数,
在R上是增函数,∴f(x)在R上是增函数,
假设存在实数m、n(m<n<0)满足题意,有
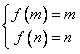 ,
,即m、n是方程f(x)=x的两个不等负根。
由
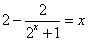 ,得
,得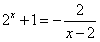 ,
,令
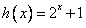 ,
,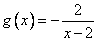 ,
,因为函数
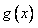 在
在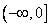 上为单调递增函数,
上为单调递增函数,∴当x<0时,
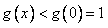 ,
,而
 ,∴
,∴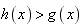 ,
,∴方程
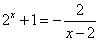 在
在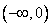 上无解,故不存在实数m、n满足题意。
上无解,故不存在实数m、n满足题意。
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 ,
, .
. 且
且 ,试讨论
,试讨论 的单调性;
的单调性; ,总
,总 使得
使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.