题目内容
【题目】已知△ABC的三个顶点A(－1,0)，B(1,0)，C(3,2)，其外接圆为⊙H.
(1)若直线l过点C，且被⊙H截得的弦长为2，求直线l的方程；
(2)对于线段BH上的任意一点P，若在以C为圆心的圆上都存在不同的两点M，N，使得点M是线段PN的中点，求⊙C的半径r的取值范围．
【答案】(1)x＝3或4x－3y－6＝0.(2)[
，
).
【解析】
试题分析：（1）先求出三角形两边的垂直平分线的方程，解联立方程组求出外心的坐标，再求出半径得出外接圆的方程，根据弦长求出圆心到直线的距离，设出直线方程利用圆心到直线的距离公式列方程求出直线的斜率，写出直线的方程，注意直线斜率不存在的情形；（2）设出点P和点N的坐标，表示出中点M的坐标，M、N满足圆C的方程，根据方程组有解说明两圆有公共点，利用两圆位置关系要求及点P满足直线BH的方程，解出半径的取值范围.
试题解析：
(1)线段AB的垂直平分线方程x＝0，线段BC的垂直平分线方程为x＋y－3＝0，
∴外接圆圆心H(0,3)，半径
，⊙H的方程x2＋(y－3)2＝10.
设圆心H到直线l的距离为d，∵直线l被⊙H截得的弦长为2，∴d＝
＝3.
当直线l垂直于x轴时，显然符合题意，即x＝3为所求；
当直线l不垂直于x轴时，设直线方程为y－2＝k(x－3)，则
＝3，解得k＝
.
综上，直线l的方程为x＝3或4x－3y－6＝0.6分
(2)直线BH的方程为3x＋y－3＝0，设P(m，n)(0≤m≤1)，N(x，y)，
∵点M是线段PN的中点，∴M(
)，
又M，N都在半径为r的⊙C上，
∴
，
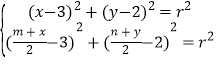即
∵此关于x，y的方程组有解，即以(3,2)为圆心，r为半径的圆与以(6－m,4－n)为圆心，2r为半径的圆有公共点，∴(2r－r)2≤(3－6＋m)2＋(2－4＋n)2≤(r＋2r)2.
又3m＋n－3＝0，∴r2≤10m2－12m＋10≤9r2对所有的m∈[0,1]成立．
而f(m)＝10m2－12m＋10在[0,1]上的值域为[
，10]，故r2≤，且10≤9r2.
又线段BH与圆C无公共点，∴(m－3)2＋(3－3m－2)2＞r2对所有的m∈[0,1]成立，
即r2＜.故⊙C的半径r的取值范围为[
).
