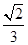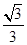题目内容
设 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不重合的平面,给定下列四个命题:
是两个不重合的平面,给定下列四个命题:
①若 ,
, ,则
,则 ;
;
②若 ,
, ,则
,则 ;
;
③若 ,
, ,则
,则 ;
;
④若 ,
, ,
, 则
则 .
.
其中真命题的是( )
| A.①和② | B.②和③ | C.③和④ | D.②和④ |
B
解析试题分析:对于①,若 ,
, ,则
,则 ,也可能
,也可能 ,故①错;对于②,根据面面垂直的判断可知②正确;对于③,因为
,故①错;对于②,根据面面垂直的判断可知②正确;对于③,因为 、
、 是两条不同的直线,当
是两条不同的直线,当 ,
, ,可知
,可知 ,故③正确;对于④,若
,故③正确;对于④,若 ,
, ,
, ,则除了
,则除了 外还有异面的情况.
外还有异面的情况.
考点:直线和平面的位置关系、平面和平面的位置关系.

练习册系列答案
相关题目
若空间三条直线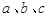 满足
满足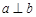 ,
,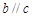 ,则直线
,则直线 与
与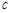 ( ).
( ).
| A.一定平行 | B.一定相交 | C.一定是异面直线 | D.一定垂直 |
在正方体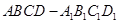 中,异面直线
中,异面直线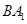 与
与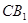 所成的角为( )
所成的角为( )
A.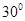 | B.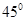 | C.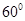 | D.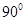 |
在空间直角坐标系中,点 ,关于
,关于 轴对称的点的坐标是( )
轴对称的点的坐标是( )
A. | B. | C. | D. |
设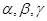 是三个互不重合的平面,
是三个互不重合的平面,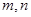 是两条不重合的直线,则下列命题中正确的是( )
是两条不重合的直线,则下列命题中正确的是( )
A.若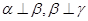 ,则 ,则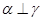 |
B.若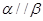 , ,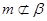 , ,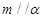 ,则 ,则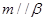 |
C.若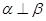 , ,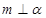 ,则 ,则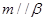 |
D.若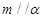 , ,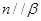 , ,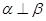 ,则 ,则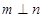 |
已知直线 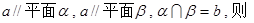
 与
与 ( )
( )
| A.相交 | B.平行 | C.异面 | D.共面或异面 |
已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题,如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
已知三条不重合的直线 ,两个不重合的平面
,两个不重合的平面 ,有下列命题:
,有下列命题:
①若 ,且
,且 ,则
,则
②若 ,且
,且 ,则
,则
③若 ,
, ,则
,则
④若 ,则
,则
其中真命题的个数是( )
| A.4 | B.3 | C.2 | D.1 |