题目内容
如图,直三棱柱 中,
中, ,
, 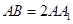 ,
, 是
是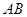 的中点,△
的中点,△ 是等腰三角形,
是等腰三角形, 为
为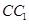 的中点,
的中点,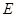 为
为 上一点.
上一点.

(1)若 ∥平面
∥平面 ,求
,求 ;
;
(2)平面 将三棱柱
将三棱柱 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
 中,
中, ,
, 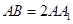 ,
, 是
是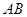 的中点,△
的中点,△ 是等腰三角形,
是等腰三角形, 为
为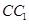 的中点,
的中点,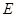 为
为 上一点.
上一点.
(1)若
 ∥平面
∥平面 ,求
,求 ;
;(2)平面
 将三棱柱
将三棱柱 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.(1)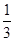 ;(2)
;(2)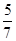 .
.
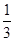 ;(2)
;(2)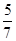 .
.试题分析:本题主要考查线线平行、线面平行、线线垂直、线面垂直、补体法、几何体的体积公式等基础知识,考查学生的空间想象能力、逻辑推理能力、计算能力.第一问,取BC中点,由中位线及平行线间的传递性,得到
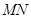 ∥
∥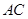 ∥
∥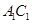 ,即
,即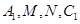 四点共面,利用线面平行的性质,得
四点共面,利用线面平行的性质,得 ∥
∥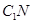 ,从而得到E是CN中点,从而得到
,从而得到E是CN中点,从而得到 的值;第二问,利用直三棱柱,得
的值;第二问,利用直三棱柱,得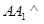 平面
平面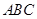 ,由
,由 ,利用线面垂直的判定,得
,利用线面垂直的判定,得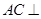 平面
平面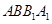 ,利用补体法求几何体
,利用补体法求几何体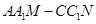 的体积,分别求出较小部分和较大部分的体积,再求比值.
的体积,分别求出较小部分和较大部分的体积,再求比值.试题解析:取
 中点为
中点为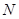 ,连结
,连结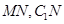 , 1分
, 1分∵
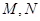 分别为
分别为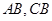 中点
中点∴
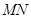 ∥
∥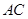 ∥
∥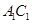 ,
,∴
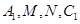 四点共面, 3分
四点共面, 3分且平面
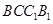
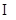 平面
平面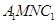
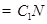
又
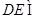 平面
平面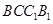 ,且
,且 ∥平面
∥平面
∴
 ∥
∥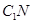
∵
 为
为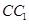 的中点,
的中点,∴
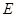 是
是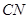 的中点, 5分
的中点, 5分∴
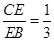 . 6分
. 6分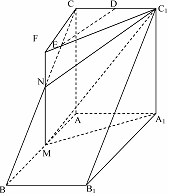
(2)因为三棱柱
 为直三棱柱,∴
为直三棱柱,∴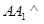 平面
平面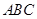 ,
,又
 ,则
,则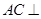 平面
平面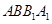
设
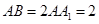 ,又三角形
,又三角形 是等腰三角形,所以
是等腰三角形,所以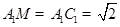 .
.如图,将几何体
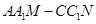 补成三棱柱
补成三棱柱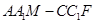
∴几何体
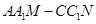 的体积为:
的体积为: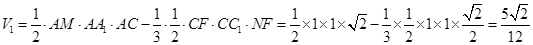 9分
9分又直三棱柱
 体积为:
体积为: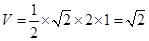 11分
11分故剩余的几何体棱台
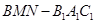 的体积为:
的体积为: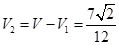
∴较小部分的体积与较大部分体积之比为:
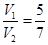 . 12分
. 12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
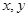 满足
满足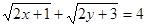 ,则
,则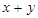 的最小值为 。
的最小值为 。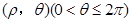 ,曲线
,曲线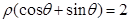 与
与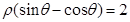 的交点的极坐标为 。
的交点的极坐标为 。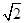 的正四棱柱的各顶点均在同一个球面上,则该球的体积为( )
的正四棱柱的各顶点均在同一个球面上,则该球的体积为( )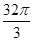
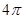
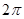
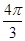
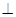 平面ABCD,则点A1的轨迹是( )
平面ABCD,则点A1的轨迹是( )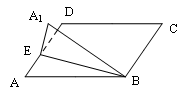
 cm2,已知球心到该截面的距离为1 cm,则该球的体积
cm2,已知球心到该截面的距离为1 cm,则该球的体积
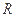 的球面,两个截面圆的半径为
的球面,两个截面圆的半径为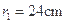 ,
,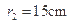 .两截面间的距离为
.两截面间的距离为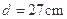 ,求球的表面积( )
,求球的表面积( )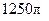
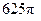
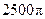
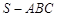 中,
中,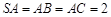 ,
,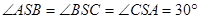 ,
,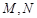 分别为
分别为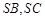 上的点,则
上的点,则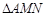 周长最小值为 .
周长最小值为 . 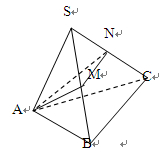
 A1B1C1D1中, P,Q是面对角线A1C1上的两个不同动点.
A1B1C1D1中, P,Q是面对角线A1C1上的两个不同动点. DQ;
DQ;