题目内容
某种海洋生物身体的长度 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)
满足如下的函数关系: .(设该生物出生时t=0)
.(设该生物出生时t=0)
(1)需经过多少时间,该生物的身长超过8米;
(2)设出生后第 年,该生物长得最快,求
年,该生物长得最快,求 的值.
的值.
 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)满足如下的函数关系:
 .(设该生物出生时t=0)
.(设该生物出生时t=0)(1)需经过多少时间,该生物的身长超过8米;
(2)设出生后第
 年,该生物长得最快,求
年,该生物长得最快,求 的值.
的值.(1)6年;(2)4或5.
试题分析:(1)求需经过多少时间,该生物的身长超过8米,实质就是解不等式
 ,不等式解集中的最小值就是本题结论;(2)首先要搞懂什么是“长得最快”,“长得最快”就是说明这一年该生物身体增长的长度最大,因此实质就是求
,不等式解集中的最小值就是本题结论;(2)首先要搞懂什么是“长得最快”,“长得最快”就是说明这一年该生物身体增长的长度最大,因此实质就是求 的最大值,即
的最大值,即 就是这个最大值,下面我们只要求出
就是这个最大值,下面我们只要求出 ,分析它的最大值是在
,分析它的最大值是在 为何值时取得,
为何值时取得,
 ,此式较繁,因此我们用换元法,设
,此式较繁,因此我们用换元法,设 ,由有
,由有

 ,它的最大值求法一般是分子分母同时除以
,它的最大值求法一般是分子分母同时除以 ,然后用基本不等式及不等式的性质得到结论.
,然后用基本不等式及不等式的性质得到结论.试题解析:(1)设
 ,即
,即 ,解得
,解得 ,
,即该生物6年后身长可超过8米; 5分
(2)设第
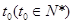 年生长最快,于是有
年生长最快,于是有 , 8分
, 8分令
 ,则
,则 ,
,令
 , 11分
, 11分等号当且仅当
 即
即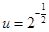 ,
, ,
, 时成立,因为
时成立,因为 ,因此
,因此 可能值为4或5,由
可能值为4或5,由 知,所求有年份为第4年和第5年,两年内各生长了
知,所求有年份为第4年和第5年,两年内各生长了 米. 14分
米. 14分
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
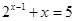 的解所在的区间( )
的解所在的区间( )



 ,函数
,函数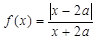 在区间
在区间 上的最大值等于
上的最大值等于 ,则
,则 的值为 .
的值为 .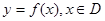 ,若存在常数
,若存在常数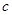 ,对任意
,对任意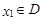 ,存在唯一
,存在唯一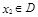 的,使得
的,使得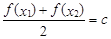 ,则称函数
,则称函数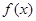 在
在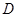 上的均值为
上的均值为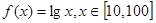 ,则函数
,则函数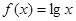 在
在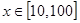 上的均值为。( )
上的均值为。( )



 ,
, ,且满足
,且满足 则
则
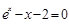 的一个根所在的区间是( )
的一个根所在的区间是( )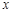
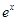
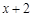
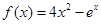 零点的个数( )
零点的个数( ) ,若关于
,若关于 的方程
的方程 有3个不同的实根
有3个不同的实根 ,则
,则 等于( )
等于( )

 ,则
,则 = .
= .