题目内容
已知在(1-2x)n的展开式中,各项的二项式系数之和是64,则(1+2x)n(1-2x2)的展开式中,x4项的系数是 .
【答案】分析:由题意求得n=6,可得(1+2x)n(1-2x2)=(1+2x)6(1-2x2)的展开式中,x4项的系数
是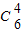 24+
24+ •22 (-2),运算求得结果.
•22 (-2),运算求得结果.
解答:解:由题意可得2n=64,解得 n=6,则(1+2x)n(1-2x2)=(1+2x)6(1-2x2)的展开式中,
x4项的系数是 24+
24+ •22 (-2)=120,
•22 (-2)=120,
故答案为 120.
点评:本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.
是
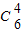 24+
24+ •22 (-2),运算求得结果.
•22 (-2),运算求得结果.解答:解:由题意可得2n=64,解得 n=6,则(1+2x)n(1-2x2)=(1+2x)6(1-2x2)的展开式中,
x4项的系数是
 24+
24+ •22 (-2)=120,
•22 (-2)=120,故答案为 120.
点评:本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目