题目内容
甲、乙二人围棋比赛,每一局甲胜乙的概率为 ,今比赛5局,记事件A为“甲恰好胜三局”,事件B为“甲恰好胜四局”,则两事件的概率( )
,今比赛5局,记事件A为“甲恰好胜三局”,事件B为“甲恰好胜四局”,则两事件的概率( )A.P(A)>P(B)
B.P(A)<P(B)
C.P(A)=P(B)
D.以上皆有可能
【答案】分析:据题意,本题是5次独立实验中,利用n次独立重复实验中事件A发生k次的概率公式得到:p(A),p(B)得到答案.
解答:解:据题意,本题是5次独立实验中,
所以利用n次独立重复实验中事件A发生k次的概率公式得到:
p(A)= ,p(B)=
,p(B)=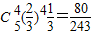 ,
,
所p(A)=p(B)
故选C.
点评:本题考查n次独立重复实验中事件A发生k次的概率公式,关键是判断出事件所属的概率模型,属于基础题.
解答:解:据题意,本题是5次独立实验中,
所以利用n次独立重复实验中事件A发生k次的概率公式得到:
p(A)=
 ,p(B)=
,p(B)=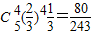 ,
,所p(A)=p(B)
故选C.
点评:本题考查n次独立重复实验中事件A发生k次的概率公式,关键是判断出事件所属的概率模型,属于基础题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目